
views
- Write a research null hypothesis as a statement that the studied variables have no relationship to each other, or that there's no difference between 2 groups.
- Write a statistical null hypothesis as a mathematical equation, such as if you're comparing group means.
- Adjust the format of your null hypothesis to match the statistical method you used to test it, such as using "mean" if you're comparing the mean between 2 groups.
What is a null hypothesis?

A null hypothesis states that there's no relationship between 2 variables. When you're doing research, you start by asking a question about the relationship between those 2 variables. Your hypothesis (also called an alternative hypothesis) is your prediction about the relationship between the 2 variables you're studying. In contrast, the null hypothesis predicts there's no relationship at all. If you're studying statistics, you'll use a mathematical format that reflects the method of data analysis you're using. Research hypothesis: States in plain language that there's no relationship between the 2 variables or there's no difference between the 2 groups being studied. Statistical hypothesis: States the predicted outcome of statistical analysis through a mathematical equation related to the statistical method you're using.
Examples of Null Hypotheses
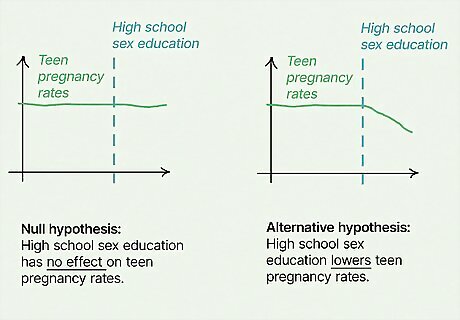
Research question: How effective is high school sex education at reducing the rate of teen pregnancy? Null hypothesis H 0 {\displaystyle H_{0}} H_{0}: High school sex education has no effect on teen pregnancy rates. Alternative hypothesis H a {\displaystyle H_{a}} {\displaystyle H_{a}}: High school sex education lowers teen pregnancy rates.
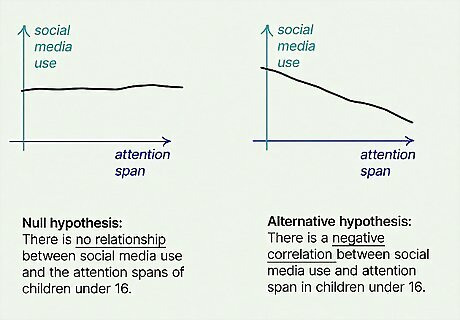
Research question: Does daily use of social media affect the attention span of children under 16? Null hypothesis H 0 {\displaystyle H_{0}} H_{0}: There is no relationship between social media use and the attention spans of children under 16. Alternative hypothesis H a {\displaystyle H_{a}} {\displaystyle H_{a}}: There is a negative correlation between social media use and attention span in children under 16.
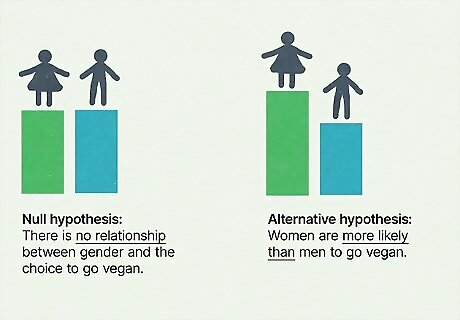
Research question: Are women more likely than men to go vegan? Null hypothesis H 0 {\displaystyle H_{0}} H_{0}: There is no relationship between gender and the choice to go vegan. Alternative hypothesis H a {\displaystyle H_{a}} {\displaystyle H_{a}}: Women are more likely than men to go vegan.
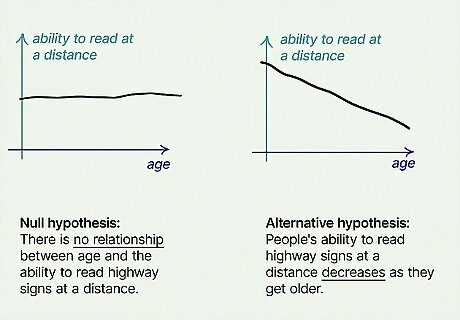
Research question: Do people have difficulty reading highway signs at a distance as they get older? Null hypothesis H 0 {\displaystyle H_{0}} H_{0}: There is no relationship between age and the ability to read highway signs at a distance. Alternative hypothesis H a {\displaystyle H_{a}} {\displaystyle H_{a}}: People's ability to read highway signs at a distance decreases as they get older.
Null Hypothesis vs. Alternative Hypothesis

Null hypotheses and alternative hypotheses are mutually exclusive. This means that if one of your hypotheses is true, the other must be false. Be careful here, though, because this isn't the same as saying they're opposites. It's possible that they could both be false. For example, your alternative hypothesis could state a positive correlation between 2 variables while your null hypothesis states there's no relationship. If there's a negative correlation, then both hypotheses are false.

Proving the null hypothesis false is a precursor to proving the alternative. If your null hypothesis states that the 2 variables have no relationship, and you prove it false, you can say this demonstrates that the 2 variables do have some relationship. But at the same time, this doesn't necessarily mean that the relationship between the 2 variables is the one you proposed in your alternative hypothesis. You need additional data or evidence to show that your alternative hypothesis is correct—proving the null hypothesis false is just the first step. In smaller studies, sometimes it's enough to show that there's some relationship and your hypothesis could be correct—you can leave the additional proof as an open question for other researchers to tackle.
How do I test a null hypothesis?
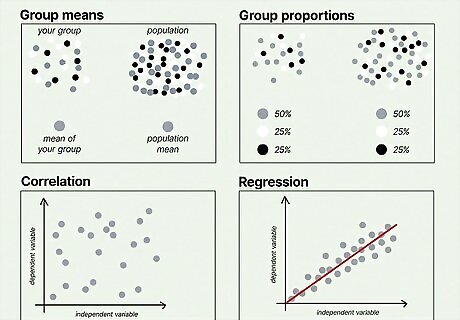
Use statistical methods on collected data to test the null hypothesis. Collect and organize your data, then choose a good statistical method to test it. There are many different methods used to analyze data—these are some of the simplest and most common: Group means: Compare the mean of the variable in your sample with the mean of the variable in the general population. Group proportions: Compare the proportion of the variable in your sample with the proportion of the variable in the general population. Correlation: Correlation analysis looks at the relationship between 2 variables—specifically, whether they tend to happen together. Regression: Regression analysis reveals the correlation between 2 variables while also controlling for the effect of other, interrelated variables.
Templates for Null Hypotheses

Group means You're testing whether the mean of a specific, dependent variable differs between 2 groups, or between a group and the population as a whole. The 2 groups are distinguished using a separate, independent variable. Research null hypothesis: There is no difference in the mean [dependent variable] between [group 1] and [group 2]. Statistical null hypothesis: μ 1 = μ 2 {\displaystyle \mu _{1}=\mu _{2}} {\displaystyle \mu _{1}=\mu _{2}} or μ 1 + μ 2 = 0 {\displaystyle \mu _{1}+\mu _{2}=0} {\displaystyle \mu _{1}+\mu _{2}=0}
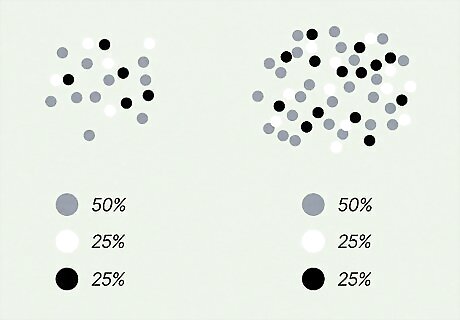
Group proportions You're testing the proportion of a specific, dependent variable in a specific population or sample as compared to a larger population. The 2 groups are distinguished using a separate, independent variable. Research null hypothesis: The proportion of [dependent variable] in [group 1] and [group 2] is the same. Statistical null hypothesis: p 1 = p 2 {\displaystyle p_{1}=p_{2}} {\displaystyle p_{1}=p_{2}}
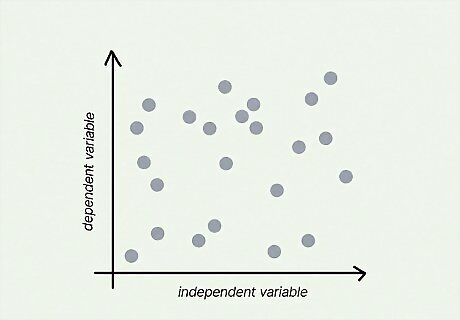
Correlation You're testing if there is a correlation between 2 variables in a specific, defined population. This is a controlled study in which there are no other variables that could possibly affect the outcome. Research null hypothesis: There is no correlation between [independent variable] and [dependent variable] in the population. Statistical null hypothesis: ρ = 0 {\displaystyle \rho =0} \rho =0
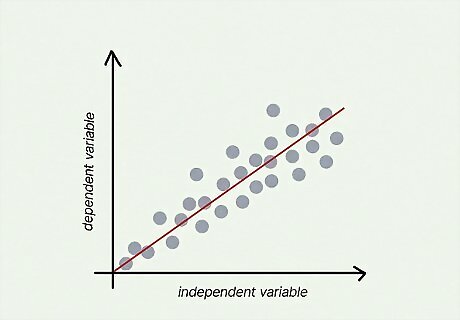
Regression You're testing if there is a correlation between 2 variables in a specific, defined population. However, there are other intertwined variables that could possibly affect the outcome. Research null hypothesis: There is no relationship between [independent variable] and [dependent variable] in the population. Statistical null hypothesis: β = 0 {\displaystyle \beta =0} {\displaystyle \beta =0}




















Comments
0 comment