
views

Take out a sheet of paper. If you are really going to stick it to the man, you might want to use something other than the everyday 8-1/2" x 11" sheets of paper.
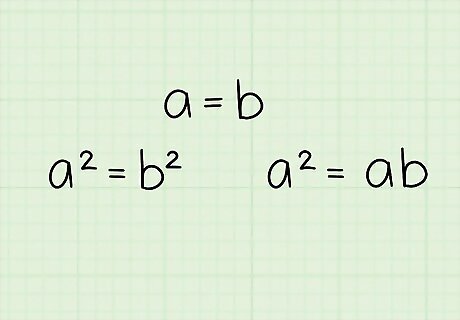
Set up your proof. At the top of the paper, write that a=b. Square both sides of the equation. a = b Rewrite this in another form. This will be your starting point for the proof. a = ab
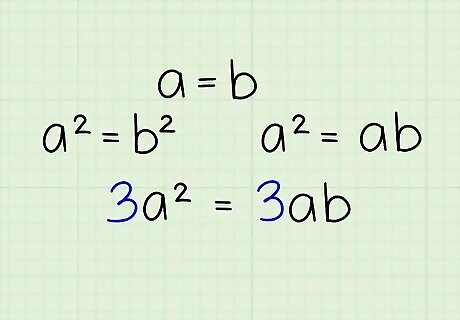
Set up a secondary equation. Simply multiply both sides of your most recent equation by 3. You will need to incorporate this into your proof later. 3a = 3ab
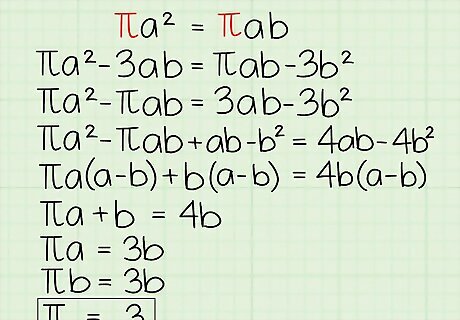
Perform the following operations: Multiply both sides of the starting point for your proof, a = ab, by π.πa = πab Subtract one (equal) half of your secondary equation, 3a = 3ab, from each side. πa - 3ab = πab - 3b Add 3ab and subtract πab on both sides. πa - πab = 3ab - 3b Add ab and subtract b on both sides. πa - πab + ab - b = 4ab - 4b Factor out common terms. πa(a-b) + b(a-b) = 4b(a-b) Remove common terms. πa + b = 4b Subtract b from both sides.πa = 3b Substitute a for b (since a = b). πb = 3b Remove common terms. π = 3
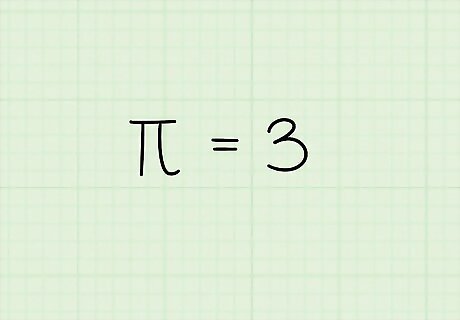
Let out a gasp of incredulity! How many years of unnecessary pain did you endure in math, calculating the area of a circle with the clearly fabricated 3.14, or, even worse, 3.1416?
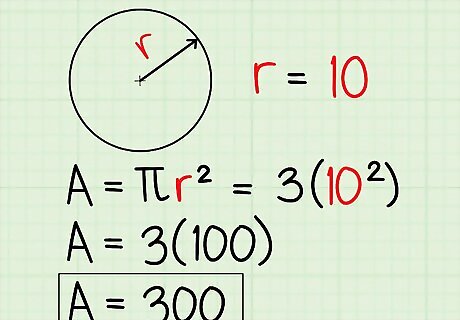
Take a moment to relish your new-found freedom by calculating areas and volumes with the new value of π: 3. Now, it's perfectly easy: Given a circle of radius 10 units, the area is π*radius, or 3*10 = 300 units. Ah, the power!
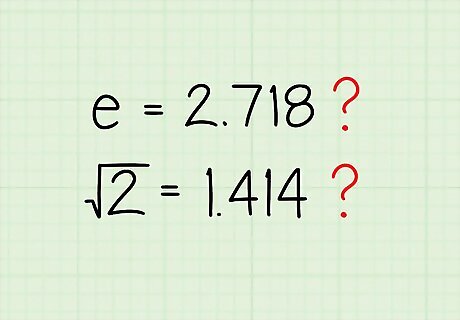
Why stop at π? You may have been one of the poor, enslaved students who also used 2.718 for e or 1.414 for the square root of 2. Be free of all of them!


















Comments
0 comment