
views
- The limit doesn’t exist when the right and left sides of a function approach different values.
- If a function approaches either negative or positive infinity as it gets closer to a value, or if it oscillates between several values, the limit does not exist.
- Find where the limit doesn’t exist by graphing the function by hand or on a calculator.
Cases When a Limit Doesn’t Exist
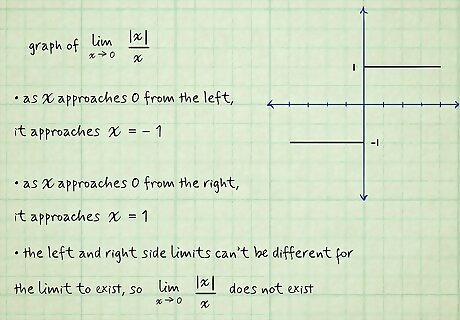
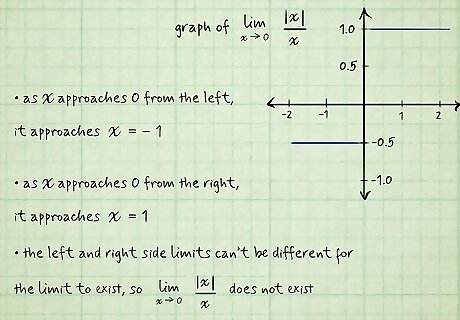
The limits are different on each side of the function. When you evaluate the limit of a function, look at how x {\displaystyle x} x approaches a value c {\displaystyle c} c from the left and right sides of the function. If the left side of the function approaches a different limit than the right side, then the limit does not exist. This means the function is not continuous throughout its entirety, which is often the case when there is a jump or gap in a function’s graph. For example, look at the graph of lim x → 0 | x | x {\displaystyle \lim _{x\to 0}{\frac {|x|}{x}}} {\displaystyle \lim _{x\to 0}{\frac {|x|}{x}}}. As x {\displaystyle x} x approaches 0 from the left, it approaches y = − 1 {\displaystyle y=-1} {\displaystyle y=-1} As x {\displaystyle x} x approaches 0 from the right, it approaches y = 1 {\displaystyle y=1} {\displaystyle y=1} The left and right side limits can’t be different for the limit to exist, so lim x → 0 | x | x {\displaystyle \lim _{x\to 0}{\frac {|x|}{x}}} {\displaystyle \lim _{x\to 0}{\frac {|x|}{x}}} does not exist. The left-hand limit is written as lim x → c − f ( x ) = L {\displaystyle \lim _{x\to c-}f(x)=L} {\displaystyle \lim _{x\to c-}f(x)=L}, where the limit of f ( x ) {\displaystyle f(x)} f(x) as x {\displaystyle x} x approaches a value c {\displaystyle c} c is the limit L {\displaystyle L} L. From the left side, you look at values of x {\displaystyle x} x that are less than c {\displaystyle c} c. The right-hand limit is written as lim x → c + f ( x ) = L {\displaystyle \lim _{x\to c+}f(x)=L} {\displaystyle \lim _{x\to c+}f(x)=L}. On the right side limit, you look at values of x {\displaystyle x} x that are greater than c {\displaystyle c} c.
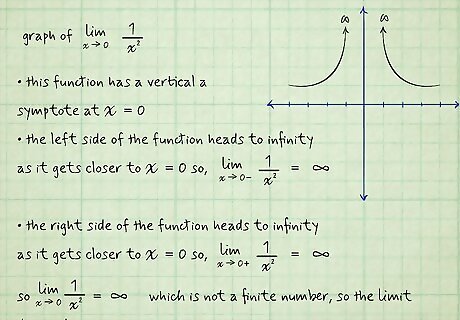
The function is boundless or doesn’t approach a finite value. Some functions have curves that approach a vertical line, called the vertical asymptote. The function never touches the line, but the distance between the curve and the line gets closer and closer to 0 as the function heads toward positive or negative infinity. If you’re evaluating lim x → c {\displaystyle \lim _{x\to c}} {\displaystyle \lim _{x\to c}} and the function has a vertical asymptote at x = c {\displaystyle x=c} {\displaystyle x=c}, then the limit does not exist. This is because at least 1 side of the function approaches infinity at x = c {\displaystyle x=c} {\displaystyle x=c}, which is not a finite, real number. For example, look at the graph of lim x → 0 1 x 2 {\displaystyle \lim _{x\to 0}{\frac {1}{x^{2}}}} {\displaystyle \lim _{x\to 0}{\frac {1}{x^{2}}}}. This function has a vertical asymptote at x = 0 {\displaystyle x=0} x=0. The left side of the function heads to infinity as it gets closer to x = 0 {\displaystyle x=0} x=0, so lim x → 0 − 1 x 2 = ∞ {\displaystyle \lim _{x\to 0-}{\frac {1}{x^{2}}}=\infty } {\displaystyle \lim _{x\to 0-}{\frac {1}{x^{2}}}=\infty }. The right side of the function heads to infinity as it gets closer to x = 0 {\displaystyle x=0} x=0, so lim x → 0 + 1 x 2 = ∞ {\displaystyle \lim _{x\to 0+}{\frac {1}{x^{2}}}=\infty } {\displaystyle \lim _{x\to 0+}{\frac {1}{x^{2}}}=\infty }. So, lim x → 0 1 x 2 = ∞ {\displaystyle \lim _{x\to 0}{\frac {1}{x^{2}}}=\infty } {\displaystyle \lim _{x\to 0}{\frac {1}{x^{2}}}=\infty } which is not a finite number, so the limit does not exist.
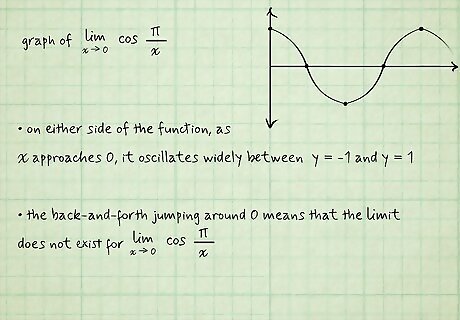
The function oscillates between more than 1 value. For the limit to exist, the function has to settle on 1 value as it approaches some value c {\displaystyle c} c. Sometimes a function tends to bounce around, or oscillate, between 2 or more values as it approaches c {\displaystyle c} c. As it gets closer to c {\displaystyle c} c, the oscillation gets faster. In these cases, the function does not settle on 1 value, so the limit does not exist. For example, look at the graph of lim x → 0 c o s ( π x ) {\displaystyle \lim _{x\to 0}cos({\frac {\pi }{x}})} {\displaystyle \lim _{x\to 0}cos({\frac {\pi }{x}})}. On either side of the function, as x {\displaystyle x} x approaches 0, it oscillates widely between y = − 1 {\displaystyle y=-1} {\displaystyle y=-1} and y = 1 {\displaystyle y=1} {\displaystyle y=1}. The back-and-forth jumping around 0 means that the limit does not exist for lim x → 0 c o s ( π x ) {\displaystyle \lim _{x\to 0}cos({\frac {\pi }{x}})} {\displaystyle \lim _{x\to 0}cos({\frac {\pi }{x}})}.
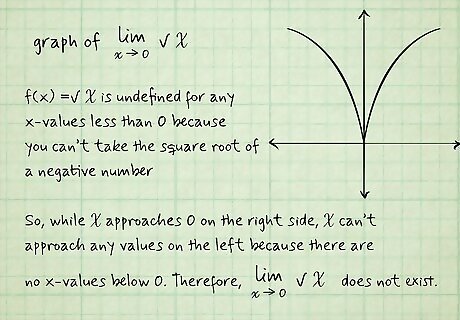
The function is only defined for some values of x. Remember how the left and right side limits have to approach the same value for the limit to exist? Some functions have x-values that are undefined or do not exist. If the function can’t approach some value c {\displaystyle c} c from 1 side because the x-values don’t exist, then the limit for that function can’t exist. For example, look at the graph of lim x → 0 x {\displaystyle \lim _{x\to 0}{\sqrt {x}}} {\displaystyle \lim _{x\to 0}{\sqrt {x}}}. f ( x ) = x {\displaystyle f(x)={\sqrt {x}}} {\displaystyle f(x)={\sqrt {x}}} is undefined for any x-values less than 0 because you can’t take the square root of a negative number (it gives you an imaginary number). So, while x {\displaystyle x} x approaches 0 on the right side, x {\displaystyle x} x can’t approach any values on the left because there are no x-values below 0. Therefore, lim x → 0 x {\displaystyle \lim _{x\to 0}{\sqrt {x}}} {\displaystyle \lim _{x\to 0}{\sqrt {x}}} does not exist.
Finding the Limit When it Doesn’t Exist
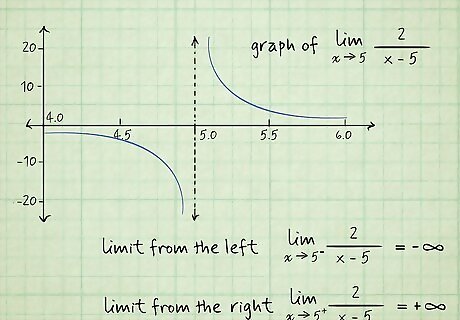
Graph the function and look at how the left and right sides approach c {\displaystyle c} c. The easiest way to evaluate a limit is to look at the behavior of the graph as x {\displaystyle x} x approaches some value c {\displaystyle c} c. Either draw the graph of the function by hand, or use a scientific calculator to plot it. Then, look at the approach of the left and right sides. Are they approaching different values? Does 1 side head toward infinity? Is the function oscillating between several values? If so, the limit doesn’t exist. For example, evaluate lim x → 5 2 x − 5 {\displaystyle \lim _{x\to 5}{\frac {2}{x-5}}} {\displaystyle \lim _{x\to 5}{\frac {2}{x-5}}}. Draw the graph on paper or plug the function into your calculator. On most scientific calculators, press the “Y =” button and enter your function. Then, press the “Graph” button. Look at how the left and right sides of the function approach c = 5 {\displaystyle c=5} {\displaystyle c=5}. The left-hand side heads towards negative infinity as it approaches, while the right side heads towards positive infinity. So, the limit does not exist.
Plug in values greater and less than c {\displaystyle c} c into the function. If you don’t have a graph of the function, take values to the right and left of c {\displaystyle c} c to see if the limits are different on each side of the function. If they are, you know that the limit can’t exist for the function. For example, evaluate lim x → 0 x | x | {\displaystyle \lim _{x\to 0}{\frac {x}{|x|}}} {\displaystyle \lim _{x\to 0}{\frac {x}{|x|}}}. Look at the left side of the function, or lim x → 0 − x | x | {\displaystyle \lim _{x\to 0-}{\frac {x}{|x|}}} {\displaystyle \lim _{x\to 0-}{\frac {x}{|x|}}}. Plug in a value to the left of 0, or that’s smaller than 0, such as -1: − 1 | − 1 | = − 1 1 = − 1 {\displaystyle {\frac {-1}{|-1|}}={\frac {-1}{1}}=-1} {\displaystyle {\frac {-1}{|-1|}}={\frac {-1}{1}}=-1}. Look at the right side of the function, or lim x → 0 + x | x | {\displaystyle \lim _{x\to 0+}{\frac {x}{|x|}}} {\displaystyle \lim _{x\to 0+}{\frac {x}{|x|}}}. Plug in a value to the right of 0, or that’s greater than 0, such as 1: 1 | 1 | = 1 1 = 1 {\displaystyle {\frac {1}{|1|}}={\frac {1}{1}}=1} {\displaystyle {\frac {1}{|1|}}={\frac {1}{1}}=1}. The limits to the left and right of lim x → 0 x | x | {\displaystyle \lim _{x\to 0}{\frac {x}{|x|}}} {\displaystyle \lim _{x\to 0}{\frac {x}{|x|}}} are different, so the limit does not exist. If you have a calculator with you, plug in several different values greater and less than x {\displaystyle x} x that are closer to c {\displaystyle c} c. For the example above, you might plug in -0.9, -0.5, 0.5, and 0.9.
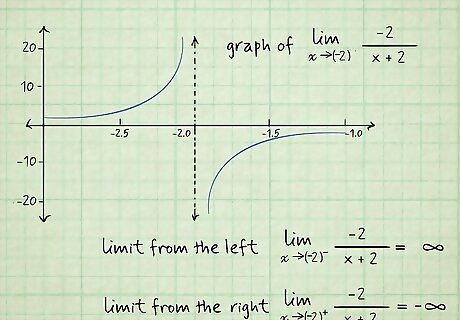
Calculate the limit using algebra. Instead of using a graph to understand how the function behaves around the limit, use your understanding of algebra. Knowing that a square root can never be negative, or that you can’t divide by 0 helps you determine whether the function is defined as x {\displaystyle x} x approaches some value c {\displaystyle c} c. If it isn’t, you know the limit does not exist. For example, evaluate lim x → − 2 − 2 x + 2 {\displaystyle \lim _{x\to -2}{\frac {-2}{x+2}}} {\displaystyle \lim _{x\to -2}{\frac {-2}{x+2}}}. If you plug -2 into the function, the denominator equals 0: − 2 − 2 + 2 = − 2 0 {\displaystyle {\frac {-2}{-2+2}}={\frac {-2}{0}}} {\displaystyle {\frac {-2}{-2+2}}={\frac {-2}{0}}}. You can’t divide by 0 and the function can’t be further simplified or factored out to solve it. But, you know that when x > − 2 {\displaystyle x>-2} {\displaystyle x>-2} in the equation, the result gets increasingly large and negative, so it’s approaching negative infinity. When x < − 2 {\displaystyle x<-2} {\displaystyle x, the result gets increasingly large and positive, so it’s approaching positive infinity. Because the left and right sides are approaching infinity, the limit does not exist.
What is a limit?
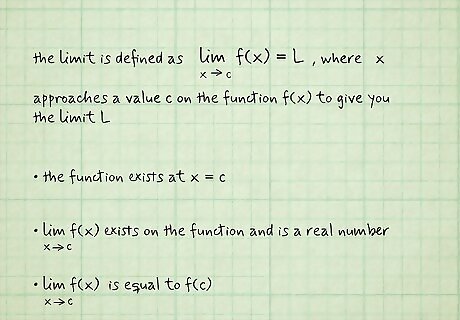
A limit is a value that describes how a function behaves at a point. In other words, the limit gives you the value that a function approaches as it gets closer to another number. Mathematically, the limit is defined as lim x → c f ( x ) = L {\displaystyle \lim _{x\to c}f(x)=L} {\displaystyle \lim _{x\to c}f(x)=L}, where x {\displaystyle x} x approaches a value c {\displaystyle c} c on the function f ( x ) {\displaystyle f(x)} f(x) to give you the limit L {\displaystyle L} L. Limits and the continuity of a function have a close relationship. Basically, a function is continuous if you can draw it without picking up your pencil. Mathematically though, a function is continuous at a point c {\displaystyle c} c if: The function exists at x = c {\displaystyle x=c} {\displaystyle x=c}. lim x → c f ( x ) {\displaystyle \lim _{x\to c}f(x)} {\displaystyle \lim _{x\to c}f(x)} exists on the function and is a real number. lim x → c f ( x ) {\displaystyle \lim _{x\to c}f(x)} {\displaystyle \lim _{x\to c}f(x)} is equal to f ( c ) {\displaystyle f(c)} {\displaystyle f(c)}.















Comments
0 comment