How to Calculate LOD Score

When progeny size is small

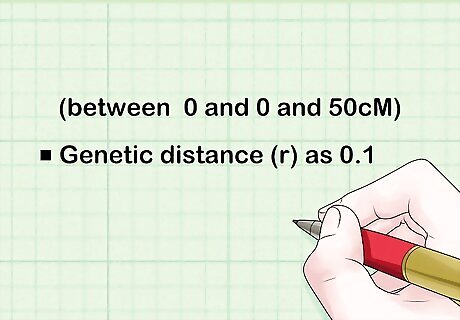
Assume a certain genetic distance between the two genes (between 0 and 0 and 50cM). Assume you take the genetic distance (r) as 0.1.

Assume that you have 13 individuals out of which 2 are recombinant. The probability of non-recombinations will be 1-r = 1-0.1 = 0.9

Since you want to track each genotype, you divide it by 2: (1-r)/2=0.45. The probability of recombinants will be r/2 = 0.1/2 = 0.05 The probability of Data if the two genes are linked is ((r/2)^R)*(((1-r)/2)^NR) where R= # of recombinants and NR = # of non-recombinants. So the probability of Data if the two genes are linked is ((0.05)^2)*((.45)^11) The probability of Data if the two genes are non-linked is (0.25)^(R+NR) = (0.25)^13 Now log of odds = (probability of Data if the two genes are linked)/(probability of Data if the two genes are non-linked). So, Log of odds = (((.05)^2)*((0.45)^11)) / ((0.25)^13) = 25.7 The LOD score will be log10(25.7) = 1.41.

Repeat this process for r as 0, 0.01, 0.03 ,0.05, 0.3 and 0.5. The highest value of LOD score you get is your correct answer. The genetic distance you've assumed is probably close to the actual distance between the two genes of interest.

When Progeny size is large

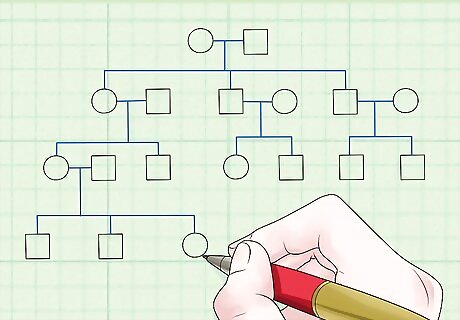
Establish a pedigree for two loci of interest. The more data you gather, the better.

Determine the number of recombinant and number of nonrecombinants. For example, suppose alleles A1 and B1 one locus 1 came from one parent, and A2 and B2 on locus 2 came from the other. Progeny inheriting A1B1 or A2B2 is non - recombinant, while those inheriting A1B2 or A2B1 are recombinant.

Calculate the probability of obtaining the results assuming the two loci are linked. This is given by ((R/(R+NR))^R)*((1-(R/(R+NR)))^NR), where R = number of recombinants, NR = number of nonrecombinants. For example, in the MNS blood group system, M and S are linked, and N and s are linked. Suppose that in 100 random individuals, 25 have MS haplotype, 30 have Ms haplotype, 6 have NS haplotype, and 39 have Ns haplotype. Since M and S are linked, and N and s are linked, MS and Ns are non - recombinants, and Ms and NS are recombinants. Thus, the number of recombinants = R = 30+ 6 = 36, while the number of nonrecombinants = NR = 25 + 39 = 64. The recombinant frequency is R/(R+NR) = 36/(36+64) = 0.36. The probability of obtaining the results assuming the two loci are linked is therefore ((0.36)^36)*((1-(0.36))^64) = 4.19187538*10^-29.

Calculate the probability of obtaining the results assuming the two loci are not linked. This is given by 0.5^(NR+R). In the example above, this is 0.5^(64+36) = 0.5^100 = 7.88860905×10^-31.

Divide the probability of obtaining the results assuming the two loci are linked (from Step 3 above), by the probability of obtaining the results assuming the two loci are not linked (from Step 4 above). For our example, this equals 4.19187538*10^-29/7.88860905×10^-31 = 53.14.

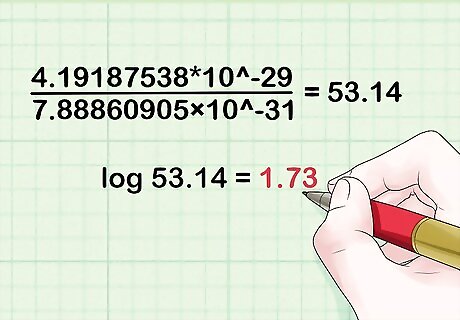
Take the base 10 logarithm of the ratio obtained above (Step 5). For the example, this equals log 53.14 = 1.73.