
views
Using the Rate as the Base

Consider an example. Suppose a bank account is started with a $1,000 deposit and the interest rate is 3% compounded annually. Find an exponential equation modeling this function.
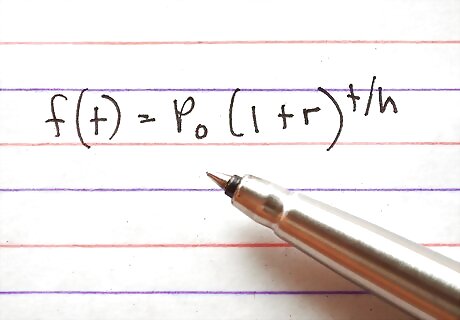
Know the basic form. The form for an exponential equation is f(t)=P0(1+r) where P0 is the initial value, t is the time variable, r is the rate and h is the number needed to ensure the units of t match up with the rate.
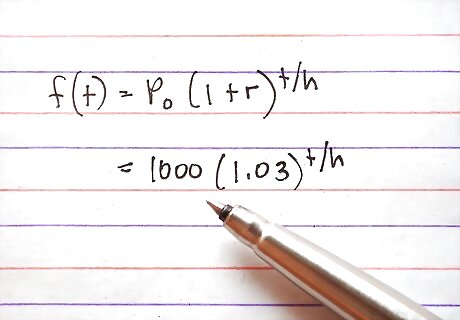
Plug in the initial value for P and the rate for r. You will have f(t)=1,000(1.03).
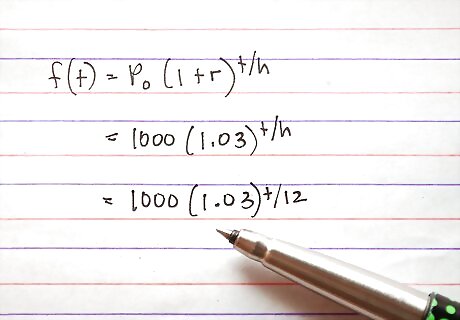
Find h. Think about your equation. Every year, the money increases by 3%, so every 12 months the money increases by 3%. Since you need to give t in months, you have to divide t by 12, so h=12. Your equation is f(t)=1,000(1.03). If the units are the same for the rate and the t increments, h is always 1.
Using "e" as the base

Understand what e is. When you use the value e as the base, you are using the "natural base." Using the natural base allows you to pull the continuous growth rate directly from the equation.

Consider an example. Suppose a 500 gram sample of an isotope of Carbon has a half life of 50 years (the half life is the amount of time for the material to decay by 50%).
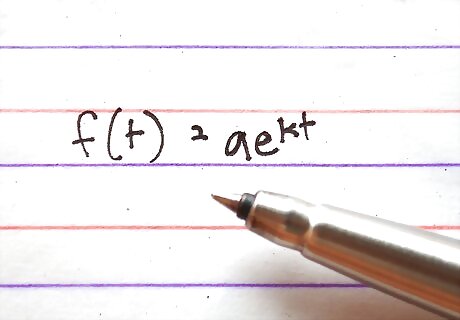
Know the basic form. The form for an exponential equation is f(t)=ae where a is the initial value, e is the base, k is the continuous growth rate, and t is the time variable.
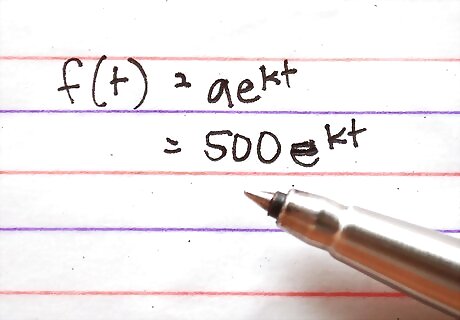
Plug in the initial value. The only value you are given that you need in the equation is the initial growth rate. So, plug it in for a to get f(t)=500e
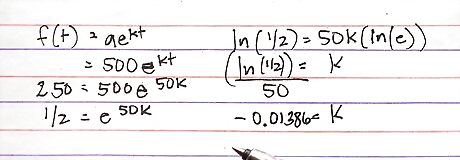
Find the continuous growth rate. The continuous growth rate is how fast the graph is changing at a particular instant. You know that in 50 years, the sample will decay to 250 grams. That can be considered a point on the graph that you can plug in. So t is 50. Plug it in to get f(50)=500e. You also know that f(50)=250, so substitute 250 for f(50) on the left hand side to obtain the exponential equation 250=500e. Now to solve the equation, first divide both sides by 500 to get: 1/2=e. Then take the natural logarithm of both sides to get: ln(1/2)=ln(e. Use the properties of logarithms to take the exponent out of the argument of the natural log and multiply it by the log. This results in ln(1/2)=50k(ln(e)). Recall that ln is the same thing as loge and that the properties of logarithms say that if the base and the argument of the logarithm are the same, the value is 1. Therefore ln(e)=1. So the equation simplifies to ln(1/2)=50k, and if you divide by 50, you learn that k=(ln(1/2))/50. Use your calculator to find the decimal approximation of k to be approximately -.01386. Notice that this value is negative. If the continuous growth rate is negative, you have exponential decay, if it is positive, you have exponential growth.

Plug in the k value. Your equation is 500e.













Comments
0 comment