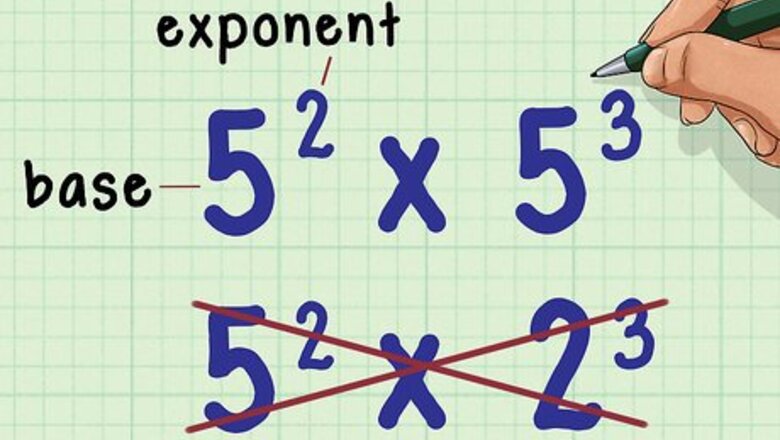
views
Multiplying Exponents with the Same Base
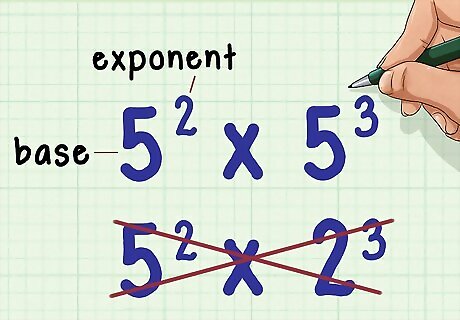
Make sure the exponents have the same base. The base is the large number in the exponential expression. You can only use this method if the expressions you are multiplying have the same base. For example, you can use this method to multiply 5 2 × 5 3 {\displaystyle 5^{2}\times 5^{3}} 5^{{2}}\times 5^{{3}}, because they both have the same base (5). On the other hand, you cannot use this method to multiply 5 2 × 2 3 {\displaystyle 5^{2}\times 2^{3}} 5^{{2}}\times 2^{{3}}, because they have different bases (5 and 2).

Add the exponents together. Rewrite the expression, keeping the same base but putting the sum of the original exponents as the new exponent. For example, if you are multiplying 5 2 × 5 3 {\displaystyle 5^{2}\times 5^{3}} 5^{{2}}\times 5^{{3}}, you would keep the base of 5, and add the exponents together: 5 2 × 5 3 {\displaystyle 5^{2}\times 5^{3}} 5^{{2}}\times 5^{{3}} = 5 2 + 3 {\displaystyle =5^{2+3}} =5^{{2+3}} = 5 5 {\displaystyle =5^{5}} =5^{{5}}
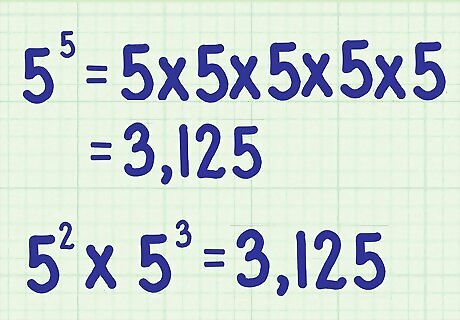
Calculate the expression. An exponent tells you how many times to multiply a number by itself. You can use a calculator to easily calculate an exponential expression, but you can also calculate by hand. For example 5 5 = 5 × 5 × 5 × 5 × 5 {\displaystyle 5^{5}=5\times 5\times 5\times 5\times 5} 5^{{5}}=5\times 5\times 5\times 5\times 5 5 5 = 3 , 125 {\displaystyle 5^{5}=3,125} 5^{{5}}=3,125So, 5 2 × 5 3 = 3 , 125 {\displaystyle 5^{2}\times 5^{3}=3,125} 5^{{2}}\times 5^{{3}}=3,125
Multiplying Exponents with Different Bases
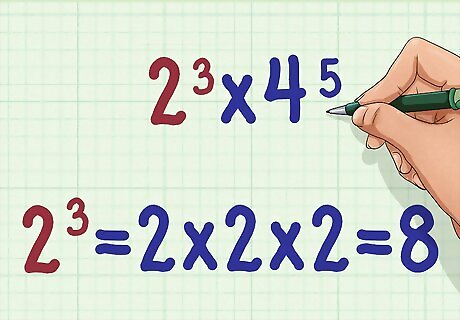
Calculate the first exponential expression. Since the exponents have different bases, there is no shortcut for multiplying them. Calculate the exponent using a calculator or by hand. Remember, an exponent tells you how many times to multiply a number by itself. For example, if you are multiplying 2 3 × 4 5 {\displaystyle 2^{3}\times 4^{5}} 2^{{3}}\times 4^{{5}}, you should note that they do not have the same base. So, you will first calculate 2 3 = 2 × 2 × 2 = 8 {\displaystyle 2^{3}=2\times 2\times 2=8} 2^{{3}}=2\times 2\times 2=8.
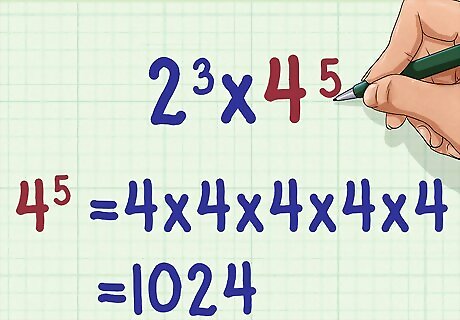
Calculate the second exponential expression. Do this by multiplying the base number by itself however many times the exponent says. For example, 4 5 = 4 × 4 × 4 × 4 × 4 = 1024 {\displaystyle 4^{5}=4\times 4\times 4\times 4\times 4=1024} 4^{{5}}=4\times 4\times 4\times 4\times 4=1024

Rewrite the problem using the new calculations. Following the same example, your new problem becomes 8 × 1024 {\displaystyle 8\times 1024} 8\times 1024.
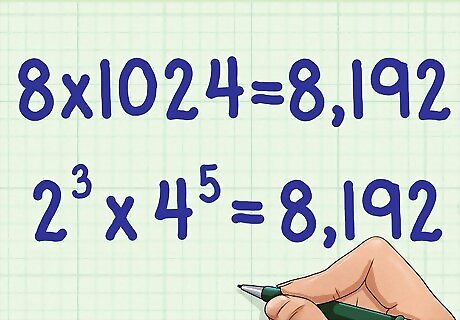
Multiply the two numbers. This will give you the final answer to the problem. For example: 8 × 1024 = 8192. {\displaystyle 8\times 1024=8192.} 8\times 1024=8192. So, 2 3 × 4 5 = 8 , 192 {\displaystyle 2^{3}\times 4^{5}=8,192} 2^{{3}}\times 4^{{5}}=8,192.
Multiplying Mixed Variables with Exponents
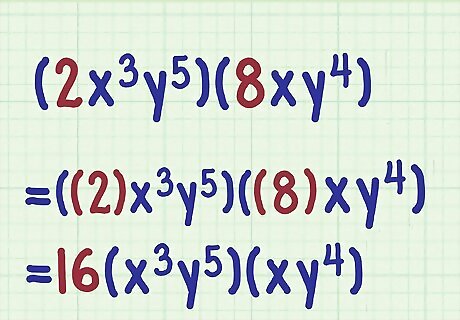
Multiply the coefficients. Multiply these as you would any whole numbers. Move the number to the outside of the parentheses. For example, if multiplying ( 2 x 3 y 5 ) ( 8 x y 4 ) {\displaystyle (2x^{3}y^{5})(8xy^{4})} (2x^{{3}}y^{{5}})(8xy^{{4}}), you would first calculate ( ( 2 ) x 3 y 5 ) ( ( 8 ) x y 4 ) = 16 ( x 3 y 5 ) ( x y 4 ) {\displaystyle ((2)x^{3}y^{5})((8)xy^{4})=16(x^{3}y^{5})(xy^{4})} ((2)x^{{3}}y^{{5}})((8)xy^{{4}})=16(x^{{3}}y^{{5}})(xy^{{4}}).
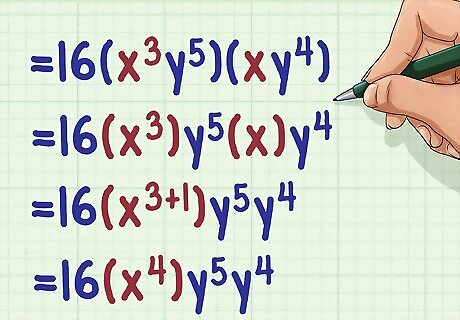
Add the exponents of the first variable. Make sure you are only adding the exponents of terms with the same base (variable). Don’t forget that if a variable shows no exponent, it is understood to have an exponent of 1. For example: 16 ( x 3 y 5 ) ( x y 4 ) = 16 ( x 3 ) y 5 ( x ) y 4 = 16 ( x 3 + 1 ) y 5 y 4 = 16 ( x 4 ) y 5 y 4 {\displaystyle 16(x^{3}y^{5})(xy^{4})=16(x^{3})y^{5}(x)y^{4}=16(x^{3+1})y^{5}y^{4}=16(x^{4})y^{5}y^{4}} 16(x^{{3}}y^{{5}})(xy^{{4}})=16(x^{{3}})y^{{5}}(x)y^{{4}}=16(x^{{3+1}})y^{{5}}y^{{4}}=16(x^{{4}})y^{{5}}y^{{4}}
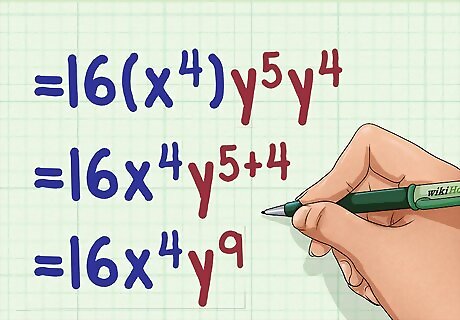
Add the exponents of the remaining variables. Take care to add exponents with the same base, and don’t forget that variables with no exponents have an understood exponent of 1. For example: 16 ( x 4 ) y 5 y 4 = 16 x 4 y 5 + 4 = 16 x 4 y 9 {\displaystyle 16(x^{4})y^{5}y^{4}=16x^{4}y^{5+4}=16x^{4}y^{9}} 16(x^{{4}})y^{{5}}y^{{4}}=16x^{{4}}y^{{5+4}}=16x^{{4}}y^{{9}}

















Comments
0 comment