
views
Multiplying by Repeated Addition

Restate the problem as an addition problem. For instance, say you are given the problem 4 ∗ 3 {\displaystyle 4*3} 4*3. This is really just another way to say “3 groups of 4,” or, for that matter, “4 groups of 3.” So, since it's the same as “3 groups of 4,” you can view the problem as 4 + 4 + 4 {\displaystyle 4+4+4} 4+4+4. Or, if you prefer, view it as 3 + 3 + 3 + 3 {\displaystyle 3+3+3+3} 3+3+3+3
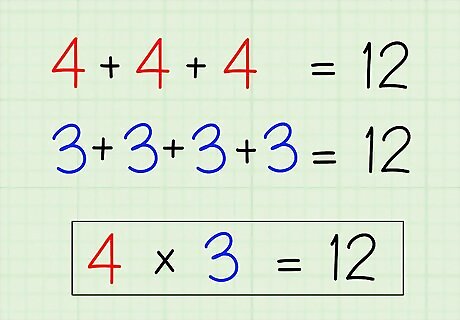
Add the repeated number together to get your answer. In the case of a simple problem like 4 ∗ 3 {\displaystyle 4*3} 4*3, just add 4 together 3 times (or, alternatively, 3 together 4 times): 4 + 4 + 4 = 12 {\displaystyle 4+4+4=12} 4+4+4=12; therefore, 4 ∗ 3 = 12 {\displaystyle 4*3=12} 4*3=12 Alternatively, 3 + 3 + 3 + 3 = 12 {\displaystyle 3+3+3+3=12} 3+3+3+3=12, so 4 ∗ 3 = 12 {\displaystyle 4*3=12} 4*3=12
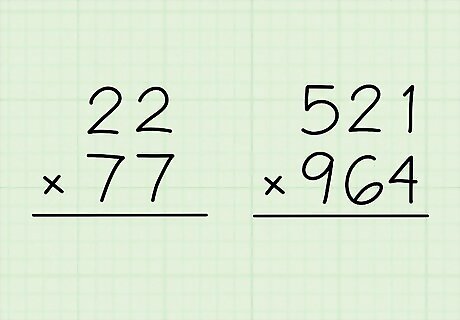
Switch to long multiplication when multiplying 2-digit or larger numbers. Technically speaking, you can find the answer to 22 ∗ 77 {\displaystyle 22*77} 22*77 or 521 ∗ 964 {\displaystyle 521*964} 521*964 through repeated addition. But it will take you way too long! For an even quicker method for multiplying smaller numbers, practice your multiplication tables (or times tables). EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Multiplication enables you to "add" numbers in a faster way. Consider buying 7 boxes, each containing 51 crayons. Instead of adding 51 seven times, multiplication (7 x 51) allows you to determine the total number of crayons quickly. Use it to solve problems efficiently rather than just memorizing facts.
Using Long Multiplication

Line up the numbers you are multiplying, larger above smaller. Place the larger number on top of the smaller number and line up the units in the hundreds, tens, and ones places. Write the multiplication sign (x or ∗ {\displaystyle *} *) to the left of the bottom number, and draw a line beneath the bottom number. You'll write your ongoing calculations below the line. In the sample problem 187 ∗ 54 {\displaystyle 187*54} 187*54, 187 goes on the top line, with 54 below it. The 5 should be in line beneath the 8, and the 4 right beneath the 7.
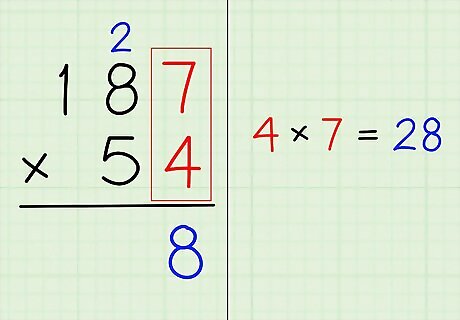
Multiply the top and bottom numbers in the ones place. In other words, multiply the bottom number's far right digit by the top number's far right digit. If your answer is two digits long (for instance, 28), carry the first digit of your answer (e.g., 2) above the digit in the tenths place of the top number. Then, place the second digit (e.g., 8) in alignment below the bottom number's far right digit. In the sample problem 187 ∗ 54 {\displaystyle 187*54} 187*54, the digits in the ones place are 4 and 7, and 4 ∗ 7 = 28 {\displaystyle 4*7=28} 4*7=28. Write the number 8 from the number 28 directly below the 4 (with the line between them), and “carry” the 2 from the number 28 by writing a small 2 over top of the 8 in 187.
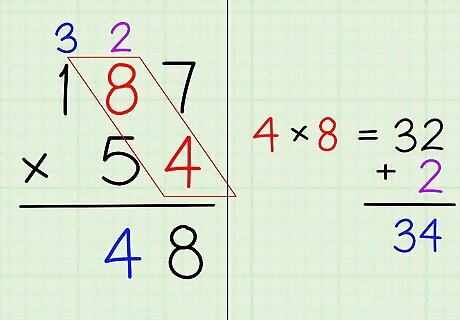
Multiply the ones place on the bottom with the tens place on top. Repeat the process you did with the digits in the ones place (on the far right), but use the digit in the tens place (second from the right) for the top number. If you have a digit carried over from multiplying the ones place digits, add it to the result of multiplying the bottom ones place and top tens place digits. In 187 ∗ 54 {\displaystyle 187*54} 187*54, 4 is in the ones place in the bottom number (54), and 8 is in the tens place in the top number (187). Compute 4 ∗ 8 = 32 {\displaystyle 4*8=32} 4*8=32, then remember to add 2 because of the number you “carried” from the previous computation—so, 32 + 2 = 34 {\displaystyle 32+2=34} 32+2=34 Place the 4 from the number 34 below the line under the 8, next to the number 8 that you wrote down in the previous step. Carry the 3 from the number 34 over the 1 in the number 187.
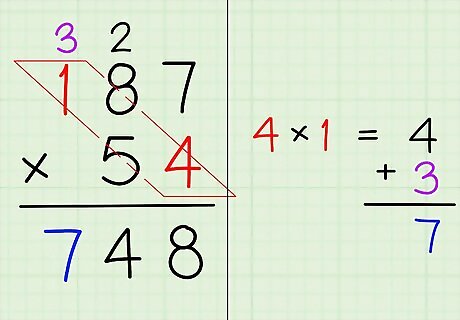
Multiply the bottom ones place with the top hundreds place. Once again, you repeat the same process as before, but this time use the digit in the ones place (far right) of the bottom number, and the digit in the hundreds place (third from the right) on the top number. And remember to add any carried over digit! In 187 ∗ 54 {\displaystyle 187*54} 187*54, the ones place for the bottom number (54) is still 4, while the hundreds place for the top number (187) is 1. Calculate 4 ∗ 1 = 4 {\displaystyle 4*1=4} 4*1=4, then add the 3 you carried from the previous calculation to get 4 + 3 = 7 {\displaystyle 4+3=7} 4+3=7 Write the 7 just to the left of the 48 below the line. It should now read 748 below the line, because you have just calculated 187 ∗ 4 = 748 {\displaystyle 187*4=748} 187*4=748. Note that if the top number had 4 or more digits, you would just repeat the process until you multiplied the number in the ones place of the bottom number with all of the digits in the top number, continuing to move from right to left.
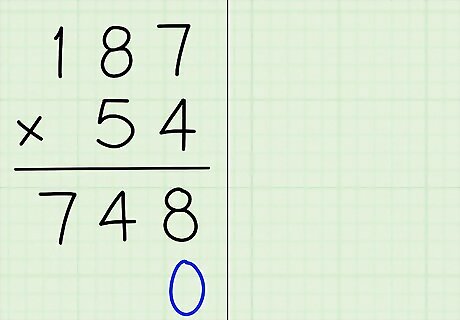
Place a zero in the ones place below your calculation (the product). The results you got from multiplying by the bottom number's ones place (far right) digit are on the first row beneath the horizontal line. Now that you're ready to move on to multiplying by the digit in the tens place, create a second row below the line and place a zero in the far right position. For 187 ∗ 54 {\displaystyle 187*54} 187*54, start a new line directly below the 748, and write 0 {\displaystyle 0} {\displaystyle 0} directly below the 8 in 748. This zero is a placeholder that shows you are moving on to multiply the tens place value. If you're multiplying larger numbers, you keep adding another zero to the right every time you add another number row below the drawn line. So, the third number row would have 00 {\displaystyle 00} 00 to the far right, the fourth number row would have 000 {\displaystyle 000} 000, and so on.

Multiply the bottom tens place with the top ones place. Once again, you're repeating the same process. This time, start with the tens digit (second from the right) of the bottom number, and the ones digit (on the far right) of the top number. In 187 ∗ 54 {\displaystyle 187*54} 187*54, the tens place in 54 is occupied by 5, and the ones place in 187 is occupied by 7. Therefore, calculate 5 ∗ 7 = 35 {\displaystyle 5*7=35} 5*7=35. Write down the 5 from 35 to the left of the zero (on the second row below the drawn line), and carry the 3 from the 35 above the 8 in the top number (187).

Multiply the bottom tens place by the top tens place. In other words, multiply the second digit from the right in the bottom number by the second digit from the right in the top number. In 187 ∗ 54 {\displaystyle 187*54} 187*54, multiply the 5 from 54 by the 8 from 187: 5 ∗ 8 = 40 {\displaystyle 5*8=40} 5*8=40. Then, remember to add the 3 you carried from the previous calculation to get 40 + 3 = 43 {\displaystyle 40+3=43} 40+3=43 Write down the 3 from 43 to the left of the 5 (giving you 350 on the bottom row), and carry the 4 from the 43 above the 1 in the top number.

Multiply tens place on the bottom with the hundreds place on the top. That is to say, multiply the second digit from the right in the bottom number by the third digit from the right in the top number. For 187 ∗ 54 {\displaystyle 187*54} 187*54, multiply the 5 from 54 by the 1 from 187. Finish this easy equation ( 5 ∗ 1 = 5 {\displaystyle 5*1=5} 5*1=5), then add the 4 that you carried from the previous computation ( 5 + 4 = 9 {\displaystyle 5+4=9} 5+4=9). Write 9 down next to the 3 to give you 9350 on the bottom row. You have done long multiplication to calculate 5 ∗ 187 = 9350 {\displaystyle 5*187=9350} 5*187=9350.

Add both products (number rows) below the drawn line. You just need to do some quick addition, and you'll be all done: Add the digits in the far right columns, 8 + 0 = 8 {\displaystyle 8+0=8} 8+0=8, draw another horizontal line below 9350, and write 8 to the far right just below the zero in 9350. Add the digits in the second column from the right, 4 + 5 = 9 {\displaystyle 4+5=9} 4+5=9, and write 9 to the left of the 8 in the bottom row. Add the digits in the third column from the right, 7 + 3 = 10 {\displaystyle 7+3=10} 7+3=10, write 0 {\displaystyle 0} {\displaystyle 0} just to the left of 98, and carry the 1 to above the 9 in 9350. Add the 9 in the fourth column from the right with the 1 you carried to get 9 + 1 = 10 {\displaystyle 9+1=10} 9+1=10. Write 10 to the left of 098 in the bottom row. Congratulations! 10098 {\displaystyle 10098} 10098 is the answer to 187 ∗ 54 {\displaystyle 187*54} 187*54.
Splitting 2-Digit Numbers into Tens and Ones
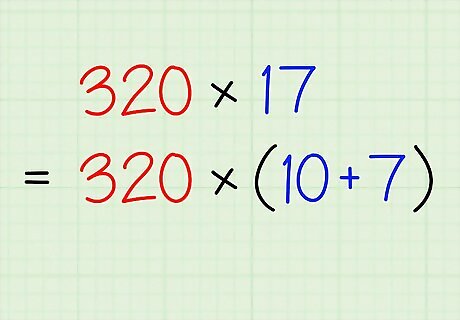
Break the smaller number in the problem into tens and ones. For instance, say you are given the problem 320 ∗ 17 {\displaystyle 320*17} 320*17. Since 17 {\displaystyle 17} 17 is the smaller number, break it into its tens ( 10 ) {\displaystyle (10)} (10) and ones ( 7 ) {\displaystyle (7)} (7) components. This shortcut method works best when the smaller number is between 10 and 19. If the smaller number is between 20 and 99, you'll have to do some extra work to figure out the tens component. As a result, you'll probably find it easier to just do traditional long multiplication. You can also use this method with a 3-digit smaller number as well—in that case, you'll need to break it up into hundreds, tens, and ones. For example, 162 would become 100, 60, and 2. Once again, though, doing standard long multiplication will likely be easier.

Create 2 separate multiplication problems. Now that you've split up the smaller number into tens and ones, use them to create 2 multiplication problems: 320 ∗ 10 {\displaystyle 320*10} 320*10 320 ∗ 7 {\displaystyle 320*7} 320*7
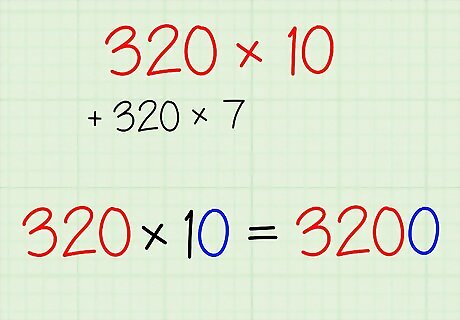
Solve the tens problem first by adding zero to the larger number. Multiplying by 10 {\displaystyle 10} 10 is always easy to do. Simply add a zero to the end of the other number. In this case, then, 320 ∗ 10 = 3200 {\displaystyle 320*10=3200} 320*10=3200. Likewise, when you multiply by 100 {\displaystyle 100} 100, you add 2 zeros, you add 3 zeros when multiplying by 1000 {\displaystyle 1000} 1000, and so on.

Solve the ones problem separately. In the current example, the ones problem is 320 ∗ 7 {\displaystyle 320*7} 320*7. Your best bet here is probably to do a fairly straightforward example of long multiplication: Write down 320 {\displaystyle 320} 320, then write 7 {\displaystyle 7} 7 just beneath it, aligned directly below the zero. Draw a 3-digit long line under the 7 {\displaystyle 7} 7. Multiply 7 {\displaystyle 7} 7 and each digit of the larger number separately, working from right to left. Since 7 ∗ 0 = 0 {\displaystyle 7*0=0} 7*0=0, write a zero under the line, aligned below the 7 {\displaystyle 7} 7. Since 7 ∗ 2 = 14 {\displaystyle 7*2=14} 7*2=14, write a 4 {\displaystyle 4} 4 just to the left of the zero under the line, and write a small 1 {\displaystyle 1} 1 just above the 3 {\displaystyle 3} 3 in 320 {\displaystyle 320} 320. This is your reminder to add 1 {\displaystyle 1} 1. Multiply 7 ∗ 3 = 21 {\displaystyle 7*3=21} 7*3=21, then add 1 {\displaystyle 1} 1 (as indicated by your reminder). Write 22 {\displaystyle 22} 22 just to the left of the 3 {\displaystyle 3} 3 and zero under the line. Your answer is under the line: 320 ∗ 7 = 2240 {\displaystyle 320*7=2240} 320*7=2240
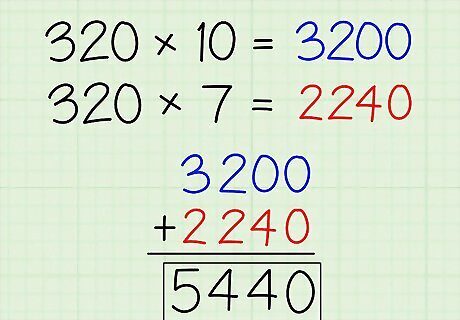
Add together the tens and ones answers. Right now, you have 320 ∗ 10 = 3200 {\displaystyle 320*10=3200} 320*10=3200 and 320 ∗ 7 = 2240 {\displaystyle 320*7=2240} 320*7=2240. To get the answer to the original equation, 320 ∗ 17 {\displaystyle 320*17} 320*17, simply add these 2 products together: Write 2240 {\displaystyle 2240} 2240 underneath 3200 {\displaystyle 3200} 3200, with the right-side zeros aligned. Draw a line underneath 2240 {\displaystyle 2240} 2240. Add each column separately, and write the sum below the line: 0 + 0 = 0 {\displaystyle 0+0=0} 0+0=0 0 + 4 = 4 {\displaystyle 0+4=4} 0+4=4 2 + 2 = 4 {\displaystyle 2+2=4} 2+2=4 3 + 2 = 5 {\displaystyle 3+2=5} 3+2=5 The answer is 5440 {\displaystyle 5440} 5440.


















Comments
0 comment