views
Bisection Construction
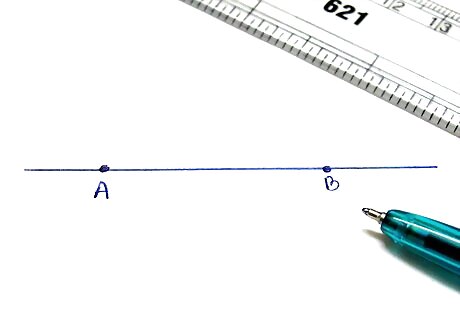
Draw one of the lines and mark two points on it.
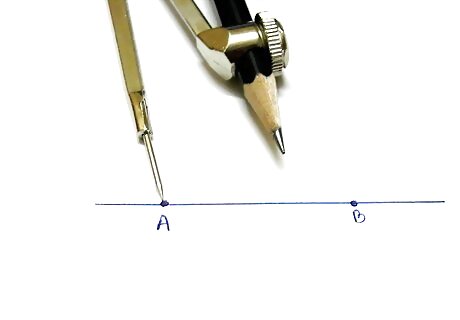
Set a compass to at least half the distance between the two points.

Use the compass to draw a circle centered around each point. The circles should intersect in two points on opposite sides of the line.
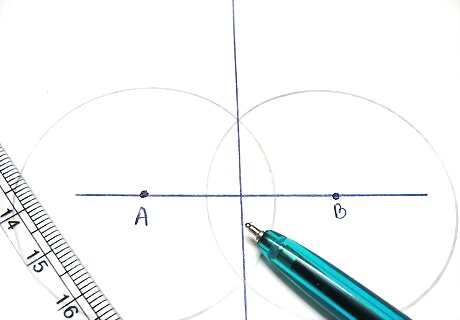
Draw a line through the two points of intersection. This is perpendicular to the original line. It also passes exactly halfway between the two points used as the centers.
Pythagorean

Draw a line of length 5 (in any units). Either use a ruler, or use a compass to mark off the same distance 5 times as shown.

Draw a circle of radius 3 around one of the endpoints.

Draw a circle of radius 4 around the other endpoint.

Draw a line from the intersection of these circles to each of the endpoints. This creates a triangle with side lengths of 3, 4, and 5. The Pythagorean Theorem states that the angle opposite the side of length 5 is a right angle.
Thales' Method

Draw a line with a straightedge.
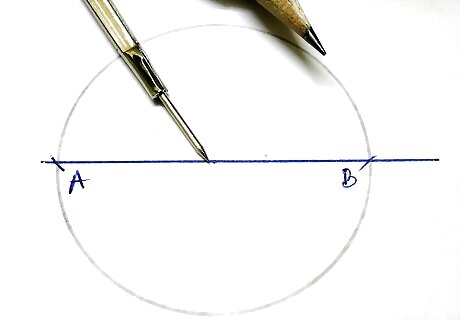
Draw a circle whose center lies on the line. Note the two endpoints of the diameter.
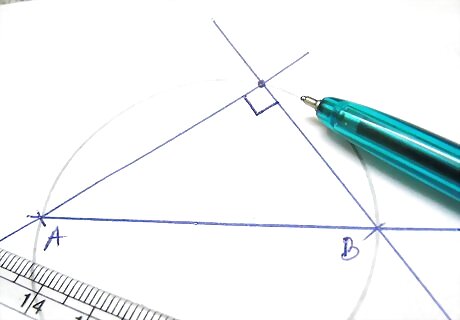
Pick any point on the circle and draw the lines connecting it to each endpoint of the diameter. These lines are perpendicular.
Coordinate Geometry
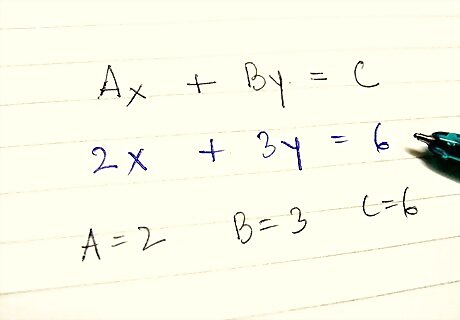
Take the equation of a line and write it in the standard form, Ax + By = C. Note the coefficients A and B (C is unimportant unless you want to ensure that the line passes through some particular point).
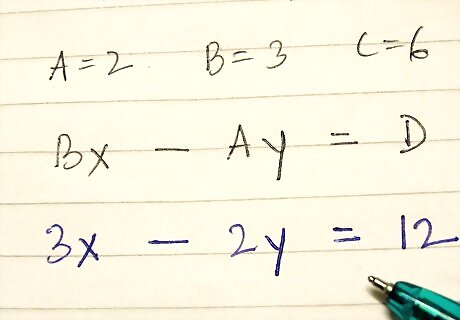
Write the equation of another line, Bx - Ay = D. Note that the coefficients of x and y have switched and one of them changed sign. D can be chosen arbitrarily as it only affects the point of intersection, not the angle.
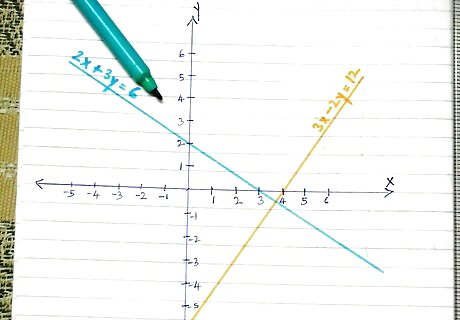
Graph both lines. They will be perpendicular.


















Comments
0 comment