
views
Learning Basic Conversion

Learn the definition of "kilo." "Kilo" is one of the most common unit prefixes, so you might already recognize it from words like "kilogram" and "kilometre". This prefix means "1000" (one thousand). Kilo- is abbreviated as "k-", so a kilogram is "kg" and a kilometre is "km".

Convert kilometres to metres. Since kilo- means 1 000, one kilometre (km) is equal to 1000 metres (m). Multiply the number of kilometres by 1 000 to get the same measurement in metres. For example, 75 kilometres = 75 k m ∗ 1 000 m k m {\displaystyle 75km*1\ 000{\frac {m}{km}}} 75km*1\ 000{\frac {m}{km}} = 75 000 metres. To make sure you've set up the conversion correctly, try reading it in plain English: 1000 m k m {\displaystyle 1000{\frac {m}{km}}} 1000{\frac {m}{km}} means "1 000 metres per kilometre".

Compare to other units. The base unit does not make any difference in this calculation. As long as you know the definition of the prefix, you can use the same math to convert between it and the base unit. Here are a couple examples: 75 kilograms (kg) = 75 k g ∗ 1 000 g k g {\displaystyle 75kg*1\ 000{\frac {g}{kg}}} 75kg*1\ 000{\frac {g}{kg}} = 75 000 grams (g). 14 kilowatts (kW) = 14 k W ∗ 1 000 W k W {\displaystyle 14kW*1\ 000{\frac {W}{kW}}} 14kW*1\ 000{\frac {W}{kW}} = 14 000 watts (W).

Learn common larger prefixes. Another common prefix is mega-, which means one million (1 000 000) and is abbreviated M. Even larger units use the prefix giga-, which means one billion (1 000 000 000) and is abbreviated G. Here are a couple conversions that use these prefixes: A 3 megawatt (MW) factory produces 3 M W ∗ 1 000 000 W M W {\displaystyle 3MW*1\ 000\ 000{\frac {W}{MW}}} 3MW*1\ 000\ 000{\frac {W}{MW}} = 3 000 000 watts (W) of power. A 2 gigajoule (GJ) explosion releases 2 G J ∗ 1 000 000 000 J G J {\displaystyle 2GJ*1\ 000\ 000\ 000{\frac {J}{GJ}}} 2GJ*1\ 000\ 000\ 000{\frac {J}{GJ}} = 2 000 000 000 joules (J) of energy.

Convert from a base unit to a larger unit. To convert to a larger unit of measurement, you'll divide by the conversion factor instead of multiplying. As always, you're less likely to make a mistake if you include the units at each point in your calculation: 65 300 metres is equal to 65 300 m ∗ 1 k m 1 000 m {\displaystyle 65\ 300m*{\frac {1\ km}{1\ 000m}}} 65\ 300m*{\frac {1\ km}{1\ 000m}} = 65.3 kilometres.

Learn prefixes with factors less than one. What if you want to measure a length shorter than one meter, or the volume of a cup smaller than one litre? That's when you use prefixes that represent a fraction of the base unit. Here are the most common prefixes of this type: centi- (c) means "one hundredth" (0.01). 1 centimetre = 0.01 metres. milli- (m) means "one thousandth" (0.001). 1 millimetre = 0.001 metres. micro- (µ) means "one millionth" (0.000 001). 1 micrometre = 0.000 001 metres. nano- (n) means "one billionth" (0.000 000 001). 1 nanometre = 0.000 000 001 metres.

Convert between the base unit and smaller units. These conversions work exactly the same. Just make sure to set up your units so they cancel out, and to keep track of decimals: Centimetres to metres: 33 centimetres = 33 c m ∗ 0.01 m c m {\displaystyle 33cm*0.01{\frac {m}{cm}}} 33cm*0.01{\frac {m}{cm}} = 0.33 metres. Metres to millimetres: 2.15 metres = 2.15 m ∗ 1 m m 0.001 m {\displaystyle 2.15m*{\frac {1mm}{0.001m}}} 2.15m*{\frac {1mm}{0.001m}} = 2150 millimetres.

Check your answer. Probably the most common mistake with these conversions is to accidentally divide instead of multiply or vice versa. There are several ways to catch this mistake: Check the units in your equation. If you set it up correctly, the original units should cancel out. For example 75 k m ∗ 1000 m k m {\displaystyle 75km*1000{\frac {m}{km}}} 75km*1000{\frac {m}{km}} gives you an answer in terms of k m ∗ m k m {\displaystyle {\frac {km*m}{km}}} {\frac {km*m}{km}}. The km units are on top and bottom, so they cancel out and leave you with m (metres). Compare the units logically. The smaller unit should always have the larger number next to it. Metres are smaller than kilometres, so it takes more of them to fill the same length. For example, a result of 75 000 metres = 75 kilometres makes sense, since a larger number of metres equals a smaller number of kilometres.
Using Powers of Ten
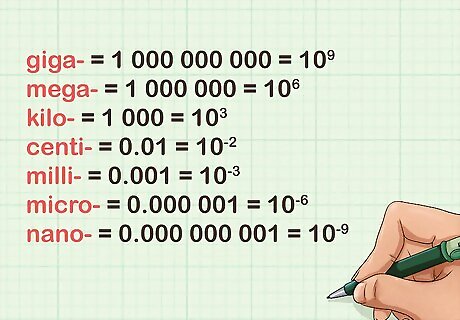
Learn the prefixes as powers of ten. Every SI prefix represents a different power of ten: 100, 1000, 0.001, and so on. Here are the most common examples written in scientific notation (standard form): giga- = 1 000 000 000 = 10 mega- = 1 000 000 = 10 kilo- = 1 000 = 10 centi- = 0.01 = 10 milli- = 0.001 = 10 micro- = 0.000 001 = 10 nano- = 0.000 000 001 = 10 You can also write a negative exponent as a fraction with a positive exponent in the denominator: 10 − 2 = 1 10 2 {\displaystyle 10^{-2}={\frac {1}{10^{2}}}} 10^{{-2}}={\frac {1}{10^{2}}}

Use scientific notation to convert to the base unit. Scientific notation makes it much easier to convert between units of very different size. No matter what the final unit you want is, you can start by converting the initial value to the base unit, using scientific notation. Example: How many centimetres are in 13.78 kilometres?The answer isn't obvious, but you do know that the kilometre is equal to 10 metres.Therefore, 13.78 km = 13.78 * 10 metres. You'll use this in the next step.
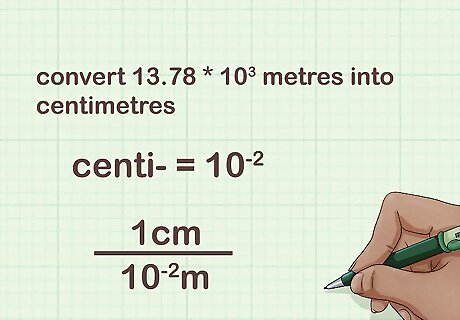
Find the conversion to your final unit. Now that you have a base unit value (with no prefix), you can set up an ordinary conversion to the final unit. Write the conversion in powers of ten notation. To continue the example, you now want to convert 13.78 * 10 metres into centimetres.The prefix centi- means 10, so there is 1 c m 10 − 2 m {\displaystyle {\frac {1cm}{10^{-2}m}}} {\frac {1cm}{10^{{-2}}m}}
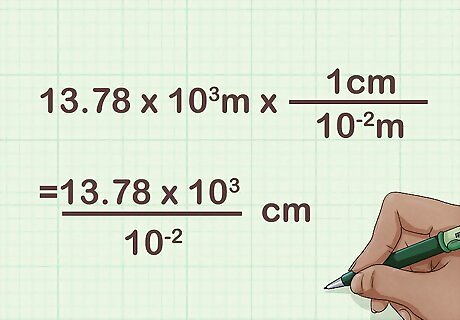
Set up the conversion as a single expression. Set up your conversion using power of ten notation for all values. This gives you a fraction that divides one power of ten by another: 13.78 ∗ 10 3 m ∗ 1 c m 10 − 2 m = 13.78 ∗ 10 3 10 − 2 {\displaystyle 13.78*10^{3}m*{\frac {1cm}{10^{-2}m}}={\frac {13.78*10^{3}}{10^{-2}}}\ } 13.78*10^{{3}}m*{\frac {1cm}{10^{{-2}}m}}={\frac {13.78*10^{{3}}}{10^{{-2}}}}\ cm
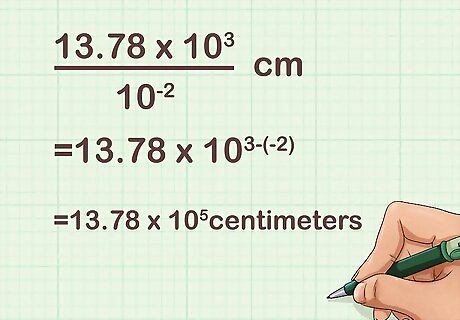
Simplify the exponents. To divide one exponential expression by the other (when they both have the same base), take the top exponent and subtract the bottom exponent. The answer is the new exponent in your answer, with the same base (which is always 10 in these conversion problems). 13.78 ∗ 10 3 10 − 2 {\displaystyle {\frac {13.78*10^{3}}{10^{-2}}}} {\frac {13.78*10^{{3}}}{10^{{-2}}}} cm = 13.78 ∗ 10 3 − ( − 2 ) = 13.78 ∗ 10 5 {\displaystyle 13.78*10^{3-(-2)}=13.78*10^{5}} 13.78*10^{{3-(-2)}}=13.78*10^{{5}} centimeters. It's usually helpful to write your answer in scientific notation (standard form): 1.378 ∗ 10 6 {\displaystyle 1.378*10^{6}} 1.378*10^{{6}} centimeters.

Simplify the formula. Once you are comfortable with this process, you can combine the whole process into a couple quick steps: Write the initial prefix and the final prefix as powers of 10. For base units without prefixes, use 10 0 {\displaystyle 10^{0}} 10^{0}. Divide the initial power of 10 by the final power of 10. (To do this, subtract the final exponent from the initial exponent.) Multiply your initial value by this answer. Example: How many centilitres (cL) are in 85 500 millilitres (mL)?The initial prefix is "milli-" = 10 − 3 {\displaystyle 10^{-3}} 10^{{-3}} and the final prefix is "centi-" = 10 − 2 {\displaystyle 10^{-2}} 10^{{-2}}. 10 − 3 10 − 2 = 10 ( − 3 ) − ( − 2 ) = 10 − 1 {\displaystyle {\frac {10^{-3}}{10^{-2}}}=10^{(-3)-(-2)}=10^{-1}} {\frac {10^{{-3}}}{10^{{-2}}}}=10^{{(-3)-(-2)}}=10^{{-1}}85 500 millilitres = 85 500 ∗ 10 − 1 {\displaystyle 85\ 500*10^{-1}} 85\ 500*10^{{-1}} centilitres.Optionally, write this in scientific notation: 8.55 ∗ 10 3 {\displaystyle 8.55*10^{3}} 8.55*10^{{3}} centilitres.


















Comments
0 comment