How to Calculate Work

Finding Work in One Dimension

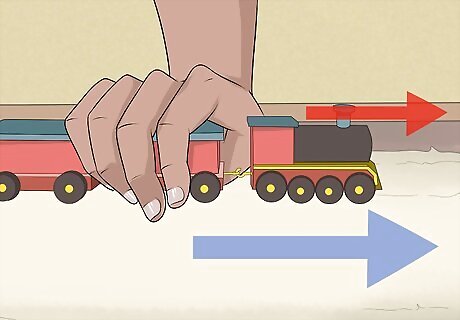
Find the direction of the force vector and the direction of motion. To start, it's important to first be able to identify both the direction the object is moving in and the direction from which force is being applied. Keep in mind that objects don't always move in line with the force being applied to them — for instance, if you pull a small wagon by its handle, you're applying a diagonal force (assuming you're taller than the wagon) to move it forward. In this section, however, we'll deal with situations in which the force and the object's displacement do have the same direction. For information on how to find the work when these things don't have the same direction, see below. To make this process easy to understand, let's follow along with an example problem. Say that a toy train car is being pulled directly forward by the train in front of it. In this case, both the force vector and the direction of the train's motion point the same way — forward. In the next few steps, we'll use this information to help find the work done on the object.

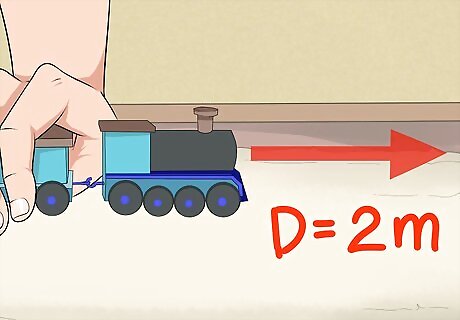
Find the displacement of your object. The first variable we need for the work formula, D, or displacement, is usually easy to find. Displacement is simply the distance that the force has caused the object to move from its starting position. In academic problems, this information is usually either given to or is possible to deduce from other information in the problem. In the real world, all you have to do to find displacement is measure the distance the object travels. Note that measures of distance must be in meters for the work formula. In our toy train example, let's say that we're finding the work performed on the train as it travels along the track. If it starts at a certain point and ends at a spot about 2 meters (6.6 ft) up the track, we can use 2 meters (6.6 ft) for our "D" value in the formula.

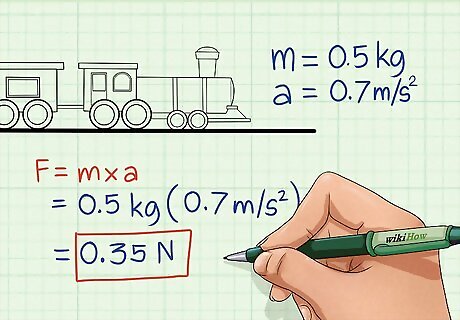
Find the force on the object. Next, find the magnitude of the force being used to move the object. This is a measure of the "strength" of the force — the bigger its magnitude, the harder it pushes the object and the quicker it accelerates. If the force's magnitude isn't provided, it can be derived from the mass and acceleration of the moving (assuming that there aren't other conflicting forces acting on it) with the formula F = M × A. Note that measures of force must be in newtons for the work formula. In our example, let's say that we don't know the magnitude of the force. However, let's say that we do know that the toy train has a mass of 0.5 kilograms and that the force is causing it to accelerate at a rate of 0.7 meters/second. In this case, we can find the magnitude by multiplying M × A = 0.5 × 0.7 = 0.35 Newtons.

Multiply Force × Distance. Once you know the magnitude of the force acting on your object and the distance it's been moved, the rest is easy. Simply multiply these two values by each other to get your value for work. It's time to solve our example problem. With a value for force of 0.35 Newtons and a value for displacement of 2 meters (6.6 ft), our answer is a single multiplication problem away: 0.35 × 2 = 0.7 joules. You may have noticed that, in the formula provided in the intro, there's an additional piece to the formula: Cosine(θ). As discussed above, in this example, the force and the direction of motion are in the same direction. This means the angle between them is 0. Since Cosine(0) = 1, we don't need to include it — we're just multiplying by 1.

Label your answer in joules. In physics, values for work (and several other quantities) are almost always given in a unit of measurement called joules. One joule is defined as one newton of force exerted over one meter, or, in other words, one newton × meter. This makes sense — since you're multiplying distance times force, it's logical that the answer that you get would have a unit of measurement equal to multiplying the units of your force and distance quantities. Note that joules also has an alternate definition — one watt of power radiated over one second. See below for a more detailed discussion of power and its relationship to work.

Finding Work With an Angled Force

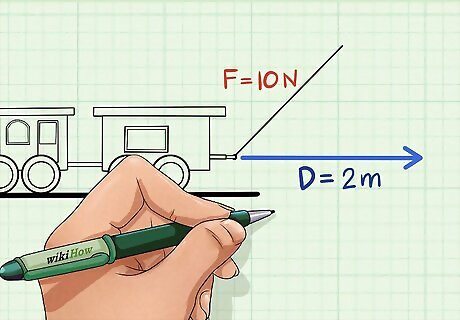
Find the force and displacement as normal. Above, we dealt with work problems in which the object is moving in the same direction as the force being applied to it. In reality, this isn't always the case. In cases where the force and the object's motion are in two different directions, the difference between these two directions must also be factored into the equation for an accurate result. To begin, find the magnitude of the force and the object's displacement as you normally would. Let's look at another example problem. In this case, let's say that we're pulling a toy train forward as in the example problem above, but that this time we're actually pulling upward at a diagonal angle. In the next step, we'll take this into account, but for now, we'll stick to the basics: the train's displacement and the magnitude of the force acting on it. For our purposes, let's say that the force has a magnitude of 10 newtons and that it's moved the same 2 meters (6.6 ft) forward as before.

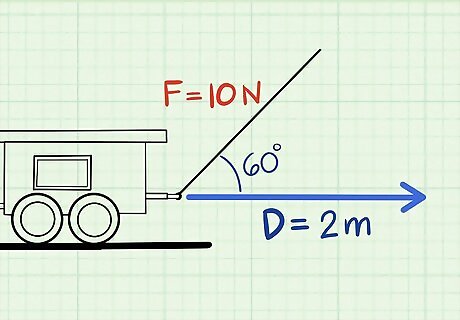
Find the angle between the force vector and the displacement. Unlike in the examples above, with a force that's in a different direction than the object's motion, it's necessary to find the difference between these two directions in the form of the angle between them. If this information isn't provided to you, you may need to measure it yourself or deduce it from other information in the problem. In our example problem, let's say that the force is being applied about 60 above the horizontal. If the train is still moving directly forward (that is, horizontally), the angle between the force vector and the train's motion is 60.

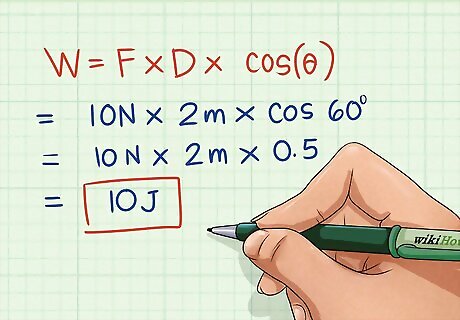
Multiply Force × Distance × Cosine(θ). Once you know the object's displacement, the magnitude of the force acting on it, and the angle between the force vector and its motion, solving is almost as easy as it is without having to take the angle into account. Simply take the cosine of the angle (this may require a scientific calculator) and multiply it by force and displacement to find your answer in joules. Let's solve our example problem. Using a calculator, we find that the cosine of 60 is 1/2. Plugging this into the formula, we can solve as follows: 10 newtons × 2 meters (6.6 ft) × 1/2 = 10 joules.

Using a Work Value

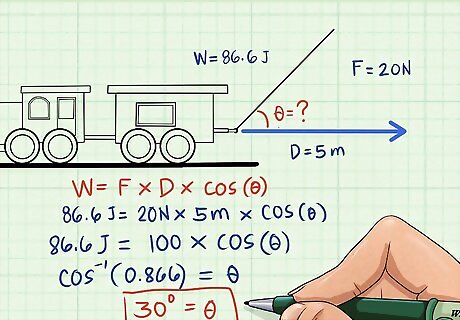
Reverse the formula to solve for distance, force, or your angle. The work formula provided above isn't just useful for finding work — it's also valuable for finding any of the variables in the equation when you already know your value for work. In these cases, simply isolate the variable you're looking for and solve according to basic algebra rules. For example, let's say that we know that our train is being pulled with 20 newtons of force at a diagonal angle over 5 meters (16.4 ft) of track to perform 86.6 joules of work. However, we don't know the angle of the force vector. To solve for the angle, we'll just isolate that variable and solve as follows: 86.6 = 20 × 5 × Cosine(θ) 86.6/100 = Cosine(θ) Arccos(0.866) = θ = 30

Divide by the time spent in motion to find power. In physics, work is closely related to another type of measurement called "power". Power is simply a way of quantifying the rate at which work is spent in a certain system over time. Thus, to find power, all you need to do is divide the work used to displace an object by the time it takes to complete the displacement. Power measurements are labeled with the unit watts (which are equal to joules per second). For instance, for the example problem in the step above, let's say that it took 12 seconds for the train to move 5 meters (16.4 ft). In this case, all we need to do is divide the work done to move it 5 meters (86.6 joules) by 12 seconds to find our answer for power: 86.6/12 = '7.22 watts.

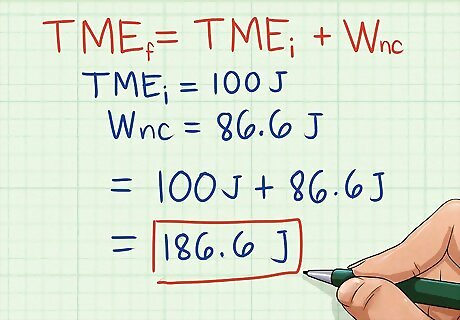
Use the formula TMEi + Wnc = TMEf to find the mechanical energy in a system. Work can also be used to find the energy held within a system. In the formula above, TMEi = the initial total mechanical energy within the system, TMEf = the final total mechanical energy within the system, and Wnc = the work performed on the system due to non-conservative forces. In this formula, if the force pushes with the direction of motion, it's positive, and if it pushes against it, it's negative. Note that both energy variables can be found with the formula (½)mv where m = mass and v = volume. For instance, for the example problem in the two steps above, let's say that the train initially had a total mechanical energy of 100 joules. Since the force in the problem is pulling the train in the direction that it's already traveling, it's positive. In this case, the train's final energy is TMEi + Wnc = 100 + 86.6 = 186.6 joules. Note that non-conservative forces are forces whose power to affect an object's acceleration depends on the path taken by the object. Friction is a good example — an object pushed over a short, direct path will feel the effects of friction for a short while, while an object pushed over a long, meandering path to the same ending location will feel more friction overall.