How to Simplify a Ratio

Basic Ratios

Look at the ratio. A ratio is an expression used to compare two quantities. A simplified ratio can be taken as is, but if a ratio has not yet been simplified, you should do so to make the quantities easier to compare and understand. In order to simplify a ratio, you divide both terms (both sides of the ratio) by the same number. This process is equivalent to reducing a fraction. Example: 15 : 21 {\displaystyle 15:21} 15:21 Note that neither number in this example is a prime number. Since that is the case, you'll need to factor both numbers to determine whether or not the two terms have any identical factors that can cancel each other in the simplification process.

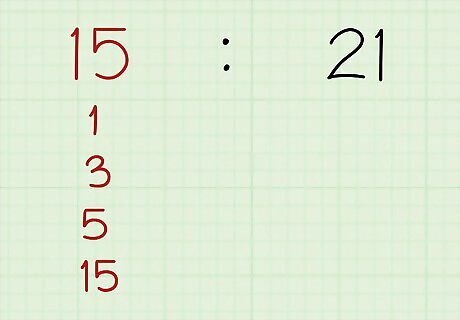
Factor the first term. A factor is a whole number (or expression) that can evenly divide into the term, leaving another whole number (or expression) as the quotient. Both terms in the ratio must share at least one factor (other than the number 1) or the ratio cannot be simplified. Before you can determine if the terms do share a factor, you must discover what the factors of each term are. Example: The number 15 has four factors: 1 , 3 , 5 , 15 {\displaystyle 1,3,5,15} 1,3,5,15 15 1 = 15 {\displaystyle {\frac {15}{1}}=15} {\frac {15}{1}}=15 15 3 = 5 {\displaystyle {\frac {15}{3}}=5} {\frac {15}{3}}=5

Factor the second term. In a separate space, list all the factors of the ratio's second term. At this point do not consider the factors of the first term; focus only on factoring this second term. Example: The number 21 has four factors: 1, 3, 7, 21 21 1 = 21 {\displaystyle {\frac {21}{1}}=21} {\frac {21}{1}}=21 21 3 = 7 {\displaystyle {\frac {21}{3}}=7} {\frac {21}{3}}=7

Find the greatest common factor. Look at the factors for both terms of the ratio. Circle, list, or otherwise identify any factors that appear in both lists. If the only shared factor is 1, then the ratio is already in its simplest form, and no further work needs to be done. If the two terms of the ratio have other shared factors, however, sort through them and identify the highest factor common to both lists. This number is the greatest common factor (GCF). Example: Both 15 and 21 share two common factors: 1 and 3 The GCF for the two terms of the original ratio is 3.

Divide both terms by the greatest common factor. Since both terms of the original ratio contain the GCF, you can divide each term by that number and come up with whole numbers as a result. Both terms must be divided by the GCF. Example: Both 15 and 21 are divided by 3. 15 3 = 5 {\displaystyle {\frac {15}{3}}=5} {\frac {15}{3}}=5 21 3 = 7 {\displaystyle {\frac {21}{3}}=7} {\frac {21}{3}}=7

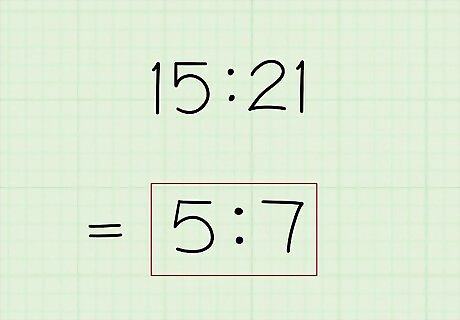
Write down the new simplified ratio. You are left with two new terms. The new ratio is equivalent in value to the original ratio, meaning that the terms in one ratio are in the same proportion as the terms in the other ratio. Note that the terms of the new ratio should not share any common factors between them (other than 1). If they do, the ratio is not yet in simplest form. Example: 5 : 7 {\displaystyle 5:7} 5:7 The point of all this is that the simplified ratio 5:7 is easier to work with than the original ratio 15:21.

Simple Algebraic Ratios

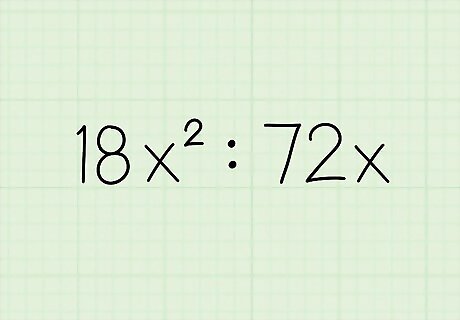
Look at the ratio. As is true of any ratio, an algebraic ratio compares two quantities, although in this case variables (letters) have been introduced into one or both terms. You will need to simplify numerical terms (as shown above) as well as any variables when finding a ratio's simplified form. Example: 18 x 2 : 72 x {\displaystyle 18x^{2}:72x} 18x^{2}:72x

Factor both terms. Remember that factors can be whole numbers which divide evenly into a given quantity. Look at the numerical values in both terms of the ratio. Write out all factors for both numerical terms in separate lists. Example: To solve this problem, you will need to find the factors of 18 and 72. The factors of 18 are: 1, 2, 3, 6, 9, 18 The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72

Find the greatest common factor. Go through both factor lists and circle, underline, or otherwise identify all of the factors shared by both lists. From this new selection of numbers, identify the highest number. This value is the greatest factor common to both of the numerical terms. Note, however, that this value represents only part of the greatest common factor within the ratio. (We still have the variables to deal with.) Example: Both 18 and 72 share several factors: 1, 2, 3, 6, 9, and 18. Of these factors, 18 is the greatest.

Divide both sides by the greatest common factor. You should be able to evenly divide both numerical terms by the GCF. Do so now, and write down the whole numbers that you get as a result. These numbers will be part of the final simplified ratio.

Example: Both 18 and 72 are now divided by the factor 18. 18 18 = 1 {\displaystyle {\frac {18}{18}}=1} {\frac {18}{18}}=1 72 18 = 4 {\displaystyle {\frac {72}{18}}=4} {\frac {72}{18}}=4

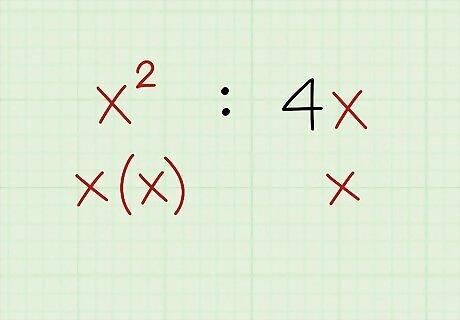
Factor out the variable if possible. Look at the variable in both terms of the ratio. If the same variable appears in both terms, it can be factored out. If there are exponents (powers) applied to the variable in both terms, deal with them now. If the exponents are the same in both terms, they cancel each other completely. If the exponents are not the same, subtract the smaller exponent from the larger. This completely cancels the variable with the smaller exponent and leaves the other variable with a diminished exponent. Understand that by subtracting one power from the other, you are essentially dividing the larger variable amount by the smaller one. Example: When examined separately, the ratio of variables was: x 2 : x {\displaystyle x^{2}:x} x^{2}:x You can factor out an x {\displaystyle x} x from both terms. The power of the first x {\displaystyle x} x is 2, and the power of the second x {\displaystyle x} x is 1. As such, one x {\displaystyle x} x can be factored out from both terms. The first term will be left with one x {\displaystyle x} x, and the second term will be left with no x {\displaystyle x} x. x ( x : 1 ) {\displaystyle x(x:1)} x(x:1) x : 1 {\displaystyle x:1} x:1

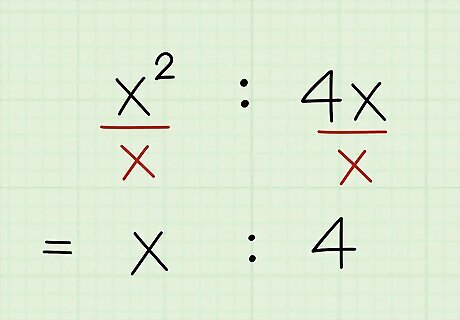
Note all of the greatest common factor. Combine the GCF of the numerical values with the GCF of the variables to find the full GCF. This GCF is the term that must be factored out of both terms of the ratio. Example: The greatest common factor in this example is 18 x {\displaystyle 18x} 18x. 18 x ⋅ ( x : 4 ) {\displaystyle 18x\cdot (x:4)} 18x\cdot (x:4)

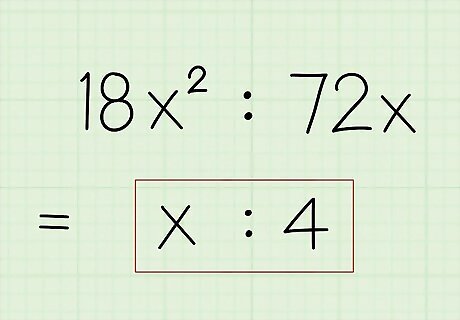
Write the simplified ratio. After you remove the GCF, the remaining ratio is the simplified form of the original ratio. This new ratio is proportionally equivalent to the original ratio. Note again that the two terms of the final ratio must not share any common factors (except 1). Example: x : 4 {\displaystyle x:4} x:4

Polynomial Ratios

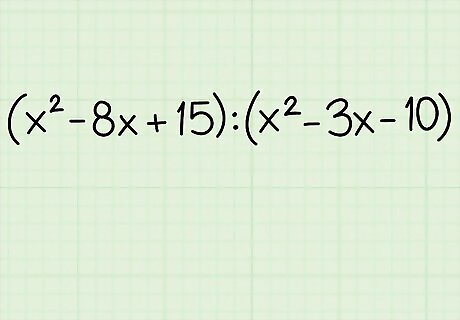
Look at the ratio. Polynomial ratios are more complex than other ratio types. There are still two quantities being compared, but the factors of those quantities are not as obvious, and the simplification may take slightly longer to perform. Nonetheless, the basic principle and steps remain the same. Example: ( x 2 − 8 x + 15 ) : ( x 2 − 3 x − 10 ) {\displaystyle (x^{2}-8x+15):(x^{2}-3x-10)} (x^{2}-8x+15):(x^{2}-3x-10)

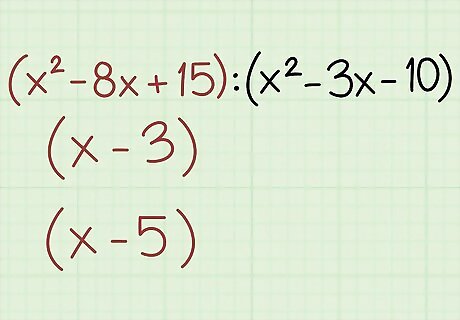
Separate the first term into factors. You'll need to factor out a polynomial from the first term. There are various methods you can use to complete this step, so you will need to use your knowledge of quadratic equations and other complex polynomials to determine the best method to use. Example: For this ratio you can use the decomposition method of factorization. x 2 − 8 x + 15 {\displaystyle x^{2}-8x+15} x^{2}-8x+15 Multiply the a and c terms together: 1 ⋅ 15 = 15 {\displaystyle 1\cdot 15=15} 1\cdot 15=15 Find two numbers that equal this number when multiplied and add up to the value of the b term: − 5 , − 3 [ − 5 ⋅ − 3 = 15 ; − 5 + − 3 = − 8 ] {\displaystyle -5,-3[-5\cdot -3=15;-5+-3=-8]} -5,-3[-5\cdot -3=15;-5+-3=-8] Substitute these two numbers into the original expression: x 2 − 5 x − 3 x + 15 {\displaystyle x^{2}-5x-3x+15} x^{2}-5x-3x+15 Factor by grouping: ( x − 3 ) ⋅ ( x − 5 ) {\displaystyle (x-3)\cdot (x-5)} (x-3)\cdot (x-5)

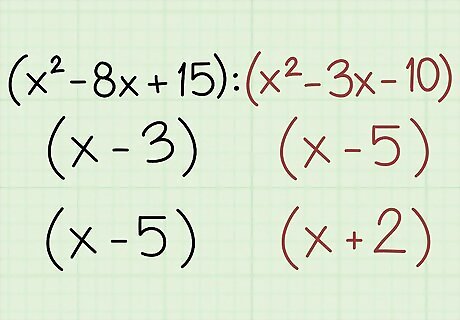
Split the second term into factors. The second term of the ratio must be broken down into factors, too. Example: Use any method desired to break down the second expression into factors: x 2 − 3 x − 10 {\displaystyle x^{2}-3x-10} x^{2}-3x-10 ( x − 5 ) ⋅ ( x + 2 ) {\displaystyle (x-5)\cdot (x+2)} (x-5)\cdot (x+2)

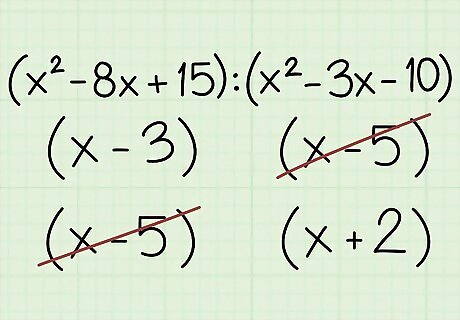
Cancel out common factors. Compare the two factored forms of the original expressions. Note that a factor in this application is any expression set in parentheses. If any of the parenthetical factors are common to both terms of the ratio, those factors can be canceled out. Example: The factored form of the ratio is written as: [ ( x − 3 ) ( x − 5 ) ] : [ ( x − 5 ) ( x + 2 ) ] {\displaystyle [(x-3)(x-5)]:[(x-5)(x+2)]} [(x-3)(x-5)]:[(x-5)(x+2)] The common factor in both terms is: ( x − 5 ) {\displaystyle (x-5)} (x-5) When the common factor is removed, the ratio can then be written as: [ ( x − 3 ) : ( x + 2 ) ] {\displaystyle [(x-3):(x+2)]} {\displaystyle [(x-3):(x+2)]}

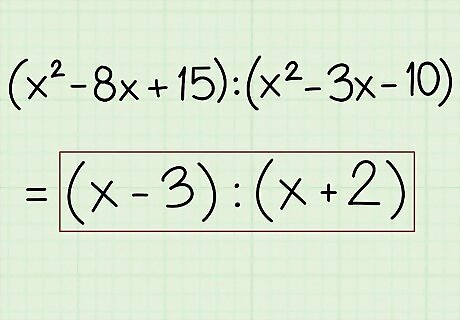
Write the simplified ratio. The two terms in the final ratio should have no factors in common. This new ratio will be equivalent in proportion to the original ratio. Example: ( x − 3 ) : ( x + 2 ) {\displaystyle (x-3):(x+2)} (x-3):(x+2)