How to Find the Volume of a Cube from Its Surface Area

Finding the Length of One Edge

Set up the formula for the surface area of a cube. The formula is s u r f a c e a r e a = 6 x 2 {\displaystyle surfacearea=6x^{2}} surfacearea=6x^{{2}}, where x {\displaystyle x} x equals the length of one edge of the cube. To find the volume of a cube, you need to multiply its three dimensions (length, width, height) together. These dimensions correspond to the length of the edges of the cube. Since all the dimensions (edges) of a cube are the same, in order to find the volume of the cube, you first have to determine the length of one of its edges. Since finding the surface area of a cube also requires the length of one edge, if you know the surface area, you can work backwards to find the length of one edge, then use the edge length to work forward to find the volume.

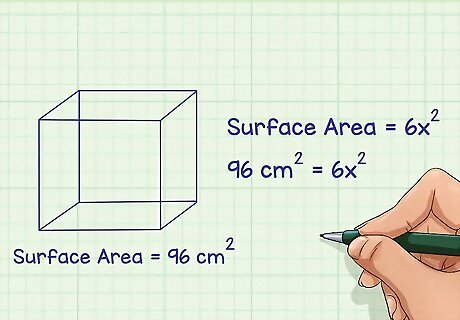
Plug the surface area of the cube into the formula. This information should be given. If you do not know the surface area of the cube, this method will not work. If you already know the length of one edge of the cube, you can skip the following steps and plug in that value for x {\displaystyle x} x into the volume of a cube formula: v o l u m e = x 3 {\displaystyle volume=x^{3}} volume=x^{{3}}. For example, if the surface area of your cube is 96 square centimeters, your formula will look like this: 96 c m 2 = 6 x 2 {\displaystyle 96cm^{2}=6x^{2}} 96cm^{{2}}=6x^{{2}}

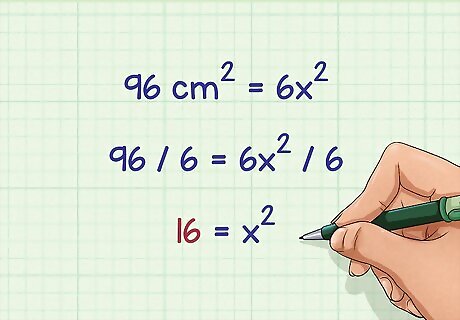
Divide the surface area by 6. This will give you the value of x 2 {\displaystyle x^{2}} x^{{2}}. For example, if the surface area of your cube is 96 square centimeters, you would divide 96 by 6: 96 c m 2 = 6 x 2 {\displaystyle 96cm^{2}=6x^{2}} 96cm^{{2}}=6x^{{2}} 96 6 = 6 x 2 6 {\displaystyle {\frac {96}{6}}={\frac {6x^{2}}{6}}} {\frac {96}{6}}={\frac {6x^{{2}}}{6}} 16 = x 2 {\displaystyle 16=x^{2}} 16=x^{{2}}

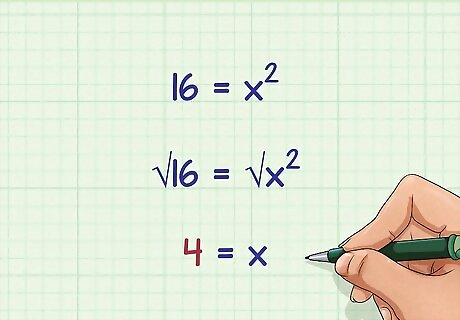
Find the square root. This will give you the value of x {\displaystyle x} x, or the length of one edge of the cube. You can find the square root using a calculator, or by hand. For complete instructions, read Calculate a Square Root by Hand. For example, if 16 = x 2 {\displaystyle 16=x^{2}} 16=x^{{2}}, then you need to find the square root of 16: 16 = x 2 {\displaystyle 16=x^{2}} 16=x^{{2}} 16 = x 2 {\displaystyle {\sqrt {16}}={\sqrt {x^{2}}}} {\sqrt {16}}={\sqrt {x^{{2}}}} 4 = x {\displaystyle 4=x} 4=xSo, the length of one edge for a cube with a surface area of 96 c m 2 {\displaystyle 96cm^{2}} 96cm^{{2}} is 4 c m {\displaystyle 4cm} 4cm.

Finding the Volume

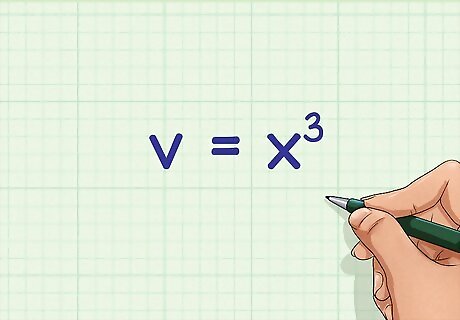
Set up the formula for the volume of a cube. The formula is v = x 3 {\displaystyle v=x^{3}} v=x^{{3}}, where v {\displaystyle v} v equals the volume of the cube, and x {\displaystyle x} x equals the length of one edge.

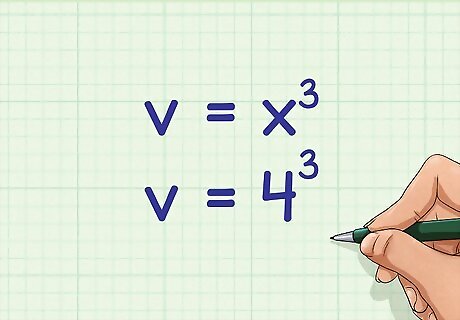
Plug the length of one edge into the formula. You should have already calculated this from the given surface area. For example, if one edge of a cube is 4 centimeters, then your formula will look like this: v = 4 3 {\displaystyle v=4^{3}} v=4^{{3}}.

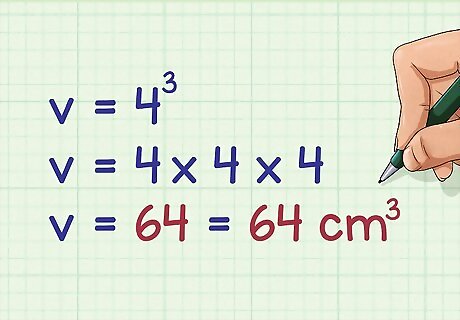
Cube the length of one edge. To do this, you can use a calculator, or simply multiply x by itself three times. This will give you the volume of your cube, in cubic units. For example, if the length of one edge is 4 centimeters, you would calculate: v = 4 3 {\displaystyle v=4^{3}} v=4^{{3}} v = 4 × 4 × 4 {\displaystyle v=4\times 4\times 4} v=4\times 4\times 4 v = 64 {\displaystyle v=64} v=64So, the volume of a cube with an edge length of 4 centimeters is 64 c m 3 {\displaystyle 64cm^{3}} 64cm^{{3}}