How to Find the Equation of a Line

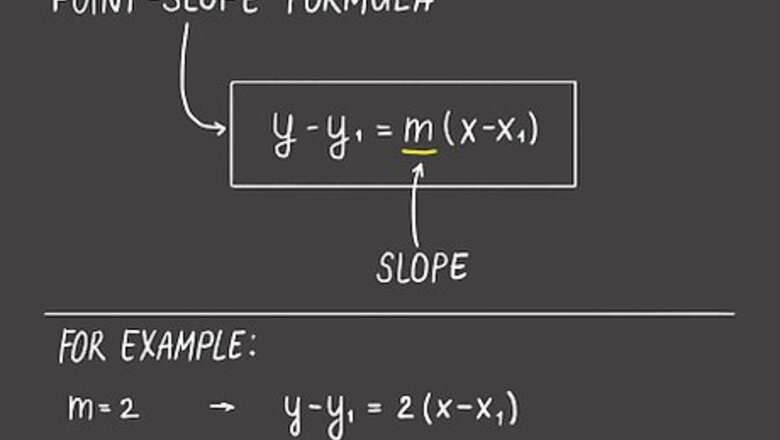
Calculating the Equation with One Point and the Slope

Plug the slope in for m in the formula y-y1 = m(x-x1). This is known as the point-slope formula. The point-slope formula uses the slope and the coordinates of a point along the line to find the y-intercept. Use the slope in place of m in y-y1 = m(x-x1). For example, if you know the slope of the line is 2, then your formula will look like this: y-y1 = 2(x-x1).

Replace x1 and y1 with the coordinates of the point. Use the coordinates you’re given as (x1, y1). Put the numbers in the corresponding spot on your formula before you start solving the equation. For example, if you know the coordinate is (4, 3), your formula will read: y-3 = 2(x-4).

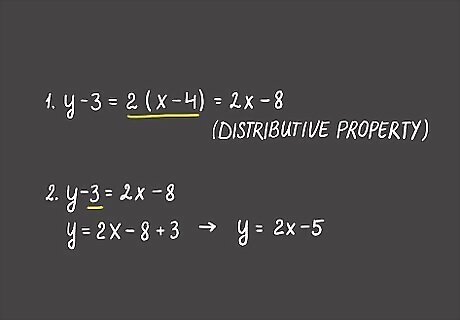
Solve the formula for y to get the final slope-intercept formula. Follow the mathematical order of operations and the distributive property to remove the x-term from parenthesis. In our example, first you’d use the distributive property to get y-3=2x-8. Then, add 3 to each side so y is by itself. The final equation for a line in slope-intercept form with a slope of 2 that contains the point (4, 3) is y = 2x-5. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher The distributive property helps you avoid repetitive calculations. You can use the distributive property to solve equations where you must multiply a number by a sum or difference. It simplifies calculations, enables expression manipulation (like factoring), and forms the basis for solving many equations.

Finding the Equation Using Two Points

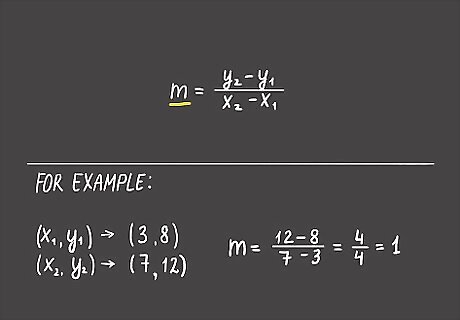
Find the slope using m = (y2-y1)/(x2-x1). The ordered pairs of the coordinates you have are listed as (x, y). Use the first set of coordinates as (x1, y1) and the second set as (x2, y2). Plug the numbers into the formula m = (y2-y1)/(x2-x1) and solve for m. For example, if your coordinates are (3, 8) and (7, 12), the formula would read: m = (12-8)/(7-3) = 4/4 = 1. In this case, your slope, or m, equals 1.

Replace the m in the slope-intercept formula with the slope you found. The slope-intercept formula of a line is written as y = mx+b, where m is the slope and b is the y-intercept (the point on the y-axis where the line crosses it). Plug the number you found for your slope in place of m. In our example, the formula would read y = 1x+b or y = x+b when you replace the slope value.

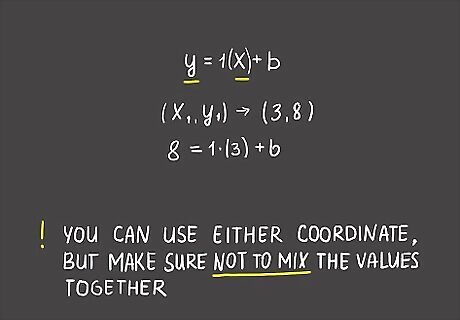
Substitute x and y for one of the points you know to solve for the y-intercept. Pick one of the ordered pairs to put into the slope-intercept formula. Put the x-value in place of x and the y-value in place of y. In this example, if you chose (3, 8) as your coordinates, then the formula would read 8 = 1(3)+b.

Solve the equation for b. Once you plug the x- and y-values as well as your slope into the formula, find the value of b in the equation. Follow the order of operations first before moving the rest of the numbers to the other side. Leave b on one side of the equation to solve it. In our example, the formula currently reads 8 = 1(3)+b. Multiply 1 and 3 together to get 8 = 3+b. Since 3 is a positive number, subtract 3 from each side to isolate b. This leaves you with 5 = b, or b = 5.

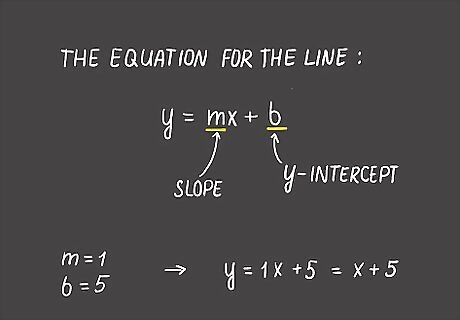
Plug in the slope and y-intercept into the slope-intercept formula to finish the equation. Once you’re finished, plug in the slope for m and the y-intercept for b. After that, you’ve found the equation for the line. For example, the equation for the line with points on (3, 8) and (7, 12) is y = 1x+5 or simply y = x+5.