How to Demonstrate Charles's Law

Demonstrating Charles’s Law with an Inflated Balloon

Add boiling water to a beaker or other container. You should leave room to put a balloon in the container as well. Adding about 100 mL of water to a 1000 mL (1 L) beaker will work in most cases. Avoid spilling the water on yourself or anyone else to avoid injury.

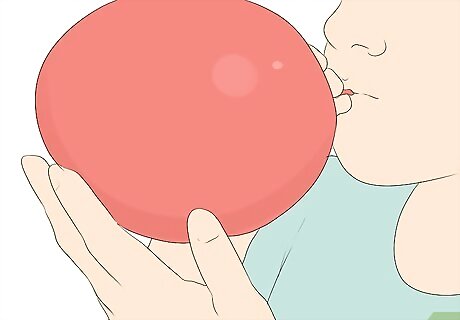
Fill a balloon with air. Blow into the balloon with your mouth, or use a pump to fill it. Do not overfill the balloon ― you want to leave room for the gas inside to expand. It is best to use a party balloon instead of a water balloon. This decreases the chance that the balloon will pop. If you plan to put the balloon into the container, do not blow it up so large that it will not fit in the opening.

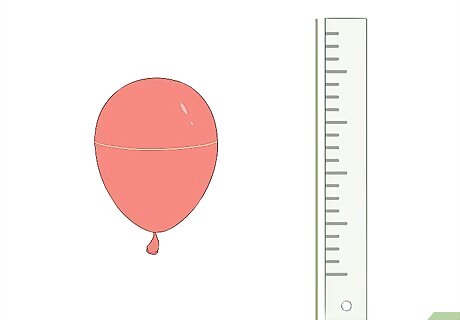
Wrap a string around the widest part of the balloon. By wrapping a piece of string around the balloon, you can get an accurate measurement of how big the balloon is in the beginning. Either mark or cut the string at at the widest part of the balloon. Remove the string from the balloon and measure it with a ruler. This measurement is the original circumference of your balloon. You will want to compare this to the size of the balloon once the air inside heats up.

Place the balloon in the container but out of the water. This will allow heat from the water to transfer to the air inside the balloon. If the balloon does not fit inside the container, another option is to put it on top of the container. The heat transfer may be a little less efficient, but it will still have the same effect on the balloon.

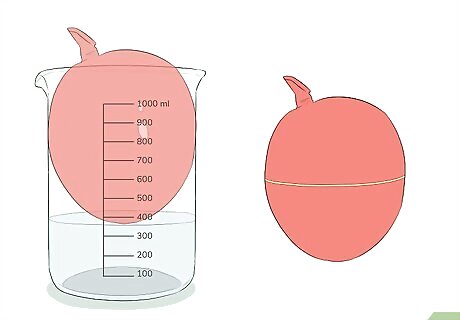
Watch as the balloon gets larger. The increase in temperature will force the air to increase its volume, thus expanding the balloon. It will look like the balloon is growing or inflating inside the container. Use another piece of string to measure the circumference of the balloon when heated. Now, you can compare it to the original circumference. Do not let the balloon expand too much, as this may cause it to pop.

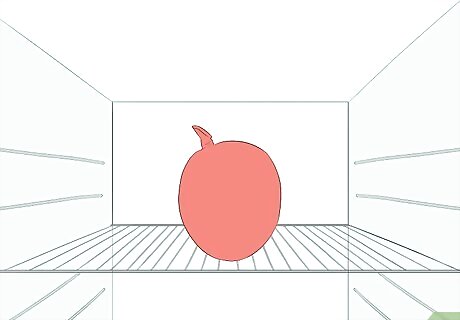
Move the balloon to the freezer. Now that you have added heat to expand the balloon, removing the heat will allow the balloon to deflate. To observe this, you will need to move the balloon from the heat source (your container of boiling water) and into a cold environment. Make sure the balloon is completely dry before placing it in the freezer. You should leave the balloon in the freezer for at least a couple of hours before removing it.

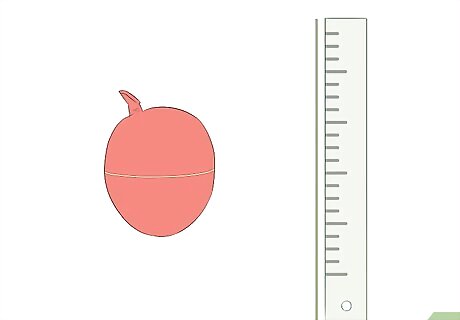
Observe the size of the balloon. When you remove the balloon from the freezer, immediately measure the circumference with a third piece of string. This way, you can compare it to your first two measurements. It should not only be smaller than it was in the warm container, but should be even smaller than it was when you first inflated it. This is because you removed heat from the gas inside the balloon, which forced the gas (and in turn the balloon) to decrease in volume.

Demonstrating Charles’s Law by Expanding and Contracting a Balloon

Add a small amount of water to an Erlenmeyer flask. You do not need to fill the flask. The less water you add, the faster you will be able to bring it to a boil. However, make sure that you do add enough water so that you don’t boil it off too quickly. About 75 mL should do nicely.

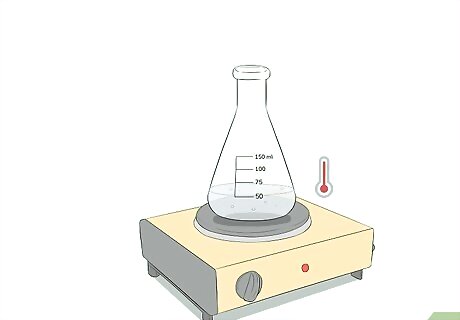
Place the flask on a hot plate or burner. This will serve as a heat source for your water. Make sure you heat the water to the boiling point. This will force air to expand out of the top of the flask and also generate water vapor to fill the balloon.

Put the open end of a balloon over the opening of the flask. Remember that the flask is being heated. You should use gloves to avoid burning your hands as you secure the balloon over the opening of the flask. Make sure that the balloon is far enough down on the neck of the flask that it does not pop off easily. It may be easier and safer to put the balloon on the flask before heating the water.

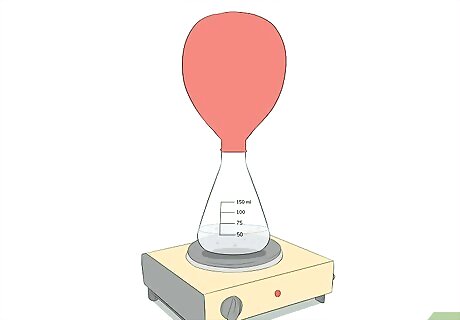
Observe the expansion of the balloon. Securing the balloon over the top of the flask will create a seal and only allow the air to expand into the balloon. This expansion of air into the balloon will cause the balloon itself to expand. Do not let the balloon get so large that it pops.

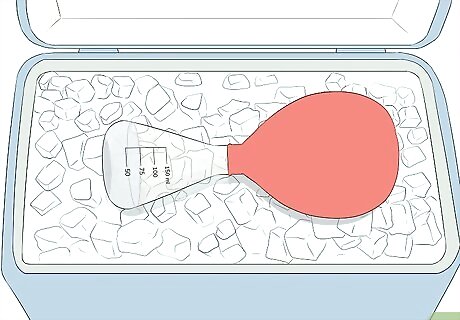
Move the flask to an ice bath. To prepare the ice bath just put water and ice into a container. This is a very easy and fast way to cool the contents of the flask. Use gloves to transfer the flask from the heat source to the ice bath.

Observe the suction on the balloon. The rapid cooling of the gas inside of the flask and balloon will cause the volume of the gas to decrease. As the volume decreases, the volume of the balloon will also decrease, causing it to shrink. As the gas cools even more and contracts even more, the volume of the gas shrinks so much that the pressure outside the flask pushes the balloon completely inside the flask.

Demonstrating Charles’s Law Mathematically

Consider the relationships at play between ideal gas properties. It was shown by Jacques Charles and then later by Joseph Gay-Lussac that the temperature of a gas is directly related to the volume when pressure and mass of the gas remain constant. This means that, for a given gas, the volume of the gas divided by the temperature of the gas will yield the same number for each volume-temperature combination.

Make sure that your units are correct. Volume should be measured in liters. Temperature should be measured in Kelvin. If your values are in different units, you should use dimensional analysis to convert them to the correct units before proceeding. Otherwise, your calculations will not be correct.

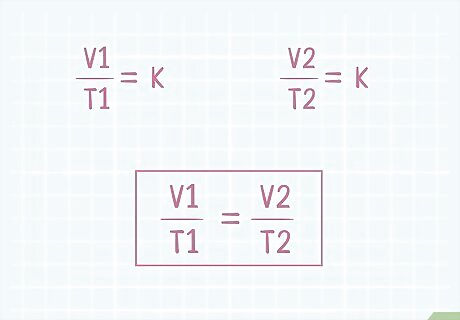
Use k to construct your equation. The initial volume (V1) of a gas divided by the initial temperature (T1) of that gas is equal to some constant, k. If the volume or temperature of that gas is altered, both values will change such that the new volume (V2) divided by the new temperature (T2) will also be equal to the same constant, k. Since V1/T1=k and V2/T2=k, V1/T1=V2/T2.

Solve the equation for the unknown variable. When given a problem to solve, you will be provided some of the measurements and asked to calculate a missing piece of the equation. Scan the problem for all given values and place them in the appropriate part of the equation. Once you have all known values in your equation, just rearrange the equation so that your unknown value is alone, and then do the arithmetic. You will have used Charles’s Law to solve your problem.