
views
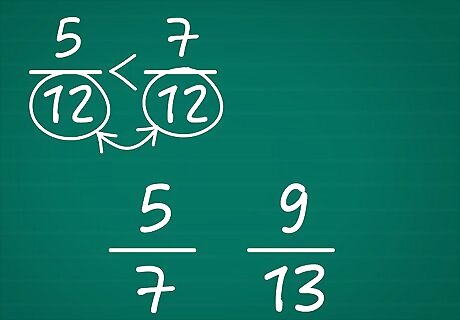
Determine whether or not the fractions have the same denominator. This is the first step to comparing fractions. The denominator is the number on the bottom of the fraction and the numerator is the number on top. For example, the fractions 5/7 and 9/13 do not have the same denominator, because 7 does not equal 13, so you'll have to take a few steps to compare them. If the denominator of the fractions is the same, then all you have to do is look at the numerator to know which fraction is greater. For example, with the fraction 5/12 and 7/12, you know that 7/12 is greater than 5/12 because 7 is greater than 5.
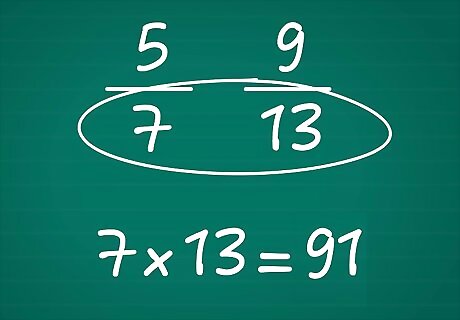
Find a common denominator. To be able to compare the fractions, you'll need to find a common denominator so you can figure out which fraction is greater. If you were adding and subtracting fractions with unlike denominators, then it would be best to find the least common denominator for the fractions. But since you're just comparing the fractions, you can just take a shortcut and multiply the denominators of both fractions to find the common denominator. 7 x 13 = 91, so the new denominator will be 91.

Change the numerators of the fractions. Now that you've changed the denominators of the fractions to 91, you'll need to change the numerators so the value of the fractions remains the same. To do this, you'll need to multiply the numerator of each fraction by the same number that you multiplied the denominator by to get 91. Here's how you do it: With the original fraction 5/7, you multiplied 7 by 13 to get a new denominator of 91, so you'll need to multiply 5 by 13 to get the new numerator. You're essentially multiplying both the numerator and the denominator of the fraction by 13/13 (which equals 1). 5/7 x 13/13 = 65/91. With the original fraction 9/13, you multiplied 13 by 7 to get a new denominator of 91, so you'll need to multiply 9 by 7 to get the new numerator. 9 x 7 = 63, so the new fraction is 63/91.
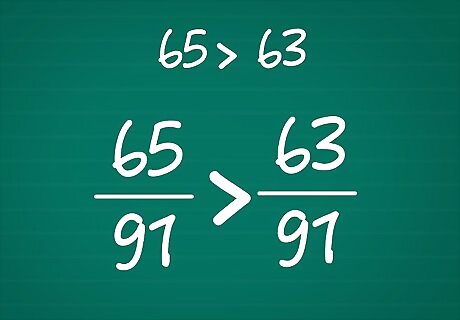
Compare the numerators of the fractions. The one with the larger numerator is the greater fraction. So, the fraction 65/91 is greater than 63/91 because 65 is greater than 63. This means that the original fraction, 5/7, is greater than 9/13. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Think about fractions as portions of a whole. Imagine dividing objects like pizzas or cakes into equal parts. Visualizing fractions this way improves comprehension, compared to relying solely on memorization. This approach can be helpful when adding, subtracting, and comparing fractions.

















Comments
0 comment