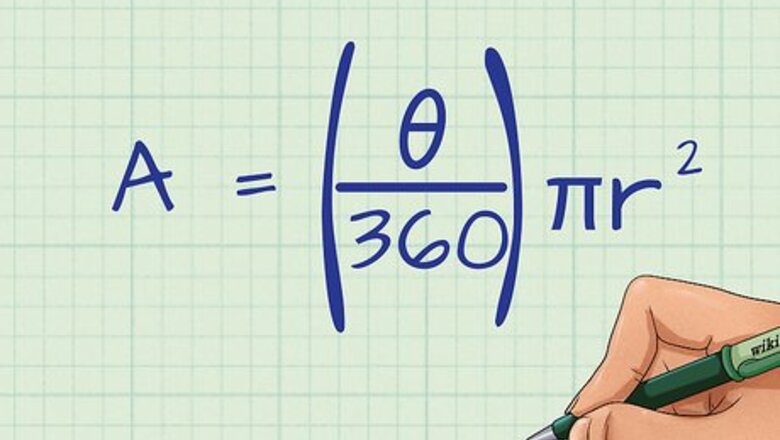
views
Calculating the Area with a Known Central Angle and Radius
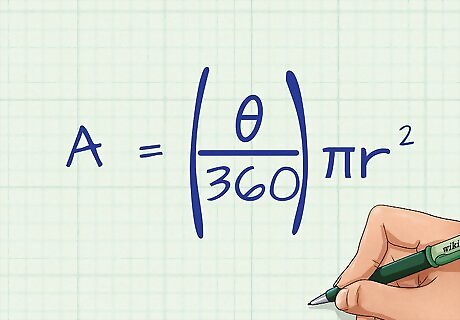
Set up the formula A = ( θ 360 ) π r 2 {\displaystyle A=\left({\frac {\theta }{360}}\right)\pi r^{2}} A=\left({\frac {\theta }{360}}\right)\pi r^{{2}}. In the formula, r = the length of the radius, and θ "Theta" = the degrees in the central angle of the sector. Remember, the area of a circle is π r 2 {\displaystyle \pi r^{2}} \pi r^{{2}}. When finding the area of a sector, you are really just calculating the area of the whole circle, and then multiplying by the fraction of the circle the sector represents. A circle is 360 degrees, so when you place the measurement of the sector's central angle over 360, it gives you the fraction of the whole circle.
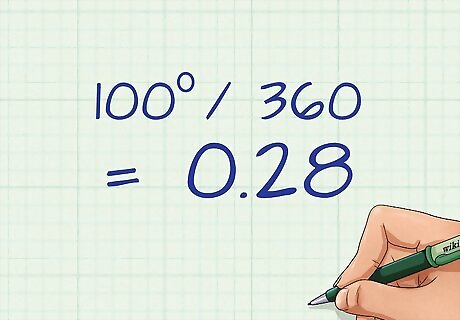
Plug the sector's central angle measurement into the formula. Divide the central angle by 360. Doing this will give you what fraction or percent of the entire circle the sector represents. For example, if the central angle is 100 degrees, you will divide 100 by 360, to get 0.28. (The area of the sector is about 28 percent of the area of the whole circle.) If you don't know the measurement of the central angle, but you know what fraction of the circle the sector is, determine the measurement of the angle by multiplying that fraction by 360. For example, if you know the sector is one-fourth of the circle, multiply 360 by one-fourth (.25) to get 90 degrees.
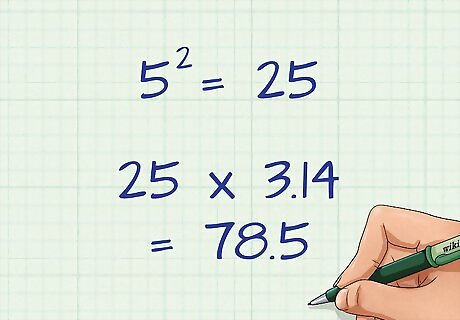
Plug the radius measurement into the formula. Square the radius, and multiply it by ???? (3.14). Doing this will allow you to calculate the area of the whole circle. For example, if the radius is 5 cm, you will square 5 to get 25, and then multiply 25 by 3.14, to get 78.5. If you don't know the length of the radius, but you know the diameter, simply divide the diameter by 2 to find the radius.
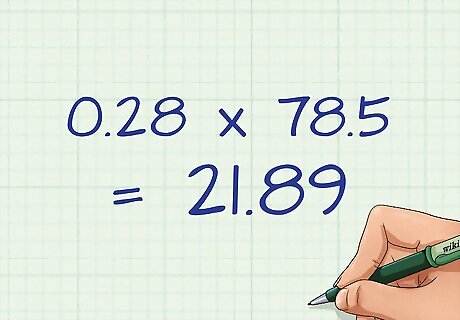
Multiply the two numbers together. Again, you will be multiplying the percent by the area of the whole circle. This gives you the area of the sector. For example, 0.28 x 78.5 = 21.89. Since you are finding the area, the answer will be in square centimetres.
Calculating the Area with a Known Arc Length and Radius
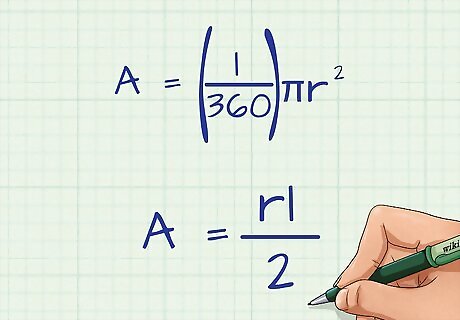
Set up the formula A = r l 2 {\displaystyle A={\frac {rl}{2}}} A={\frac {rl}{2}}. In the formula, r = the length of the radius, and l = the length of the arc. Remember the formula for finding the circumference (perimeter) of a circle is 2????r. If you know the length of the arc (which is a portion of the circumference), you can find what fraction of the circle the sector represents by comparing the arc length to the total circumference. The complete formula would be A = ( l 2 π r ) π r 2 {\displaystyle A=\left({\frac {l}{2\pi r}}\right)\pi r^{2}} A=\left({\frac {l}{2\pi r}}\right)\pi r^{{2}}, but you can simplify it to A = r l 2 {\displaystyle A={\frac {rl}{2}}} A={\frac {rl}{2}}.
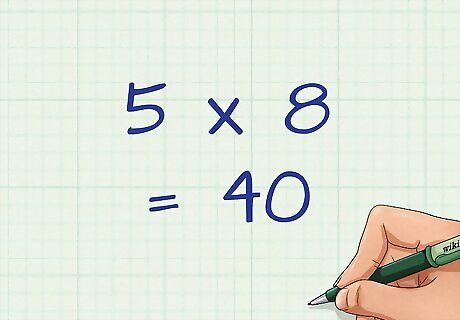
Plug in the arc length and radius into the formula. You will be multiplying these two numbers to get a new numerator. For example, if the arc length is 5 cm and the radius is 8 cm, your new numerator will be 40.
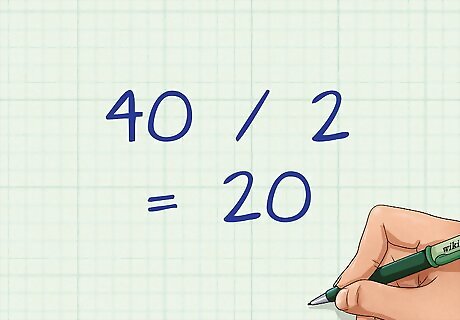
Divide by 2. You are dividing the numerator found in step two. This gives you the area of the sector. For example, 40 2 = 20 {\displaystyle {\frac {40}{2}}=20} {\frac {40}{2}}=20. Since you are finding the area, your answer will be in square centimetres.



















Comments
0 comment